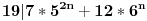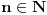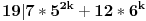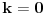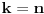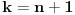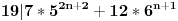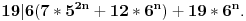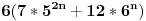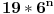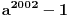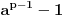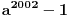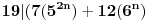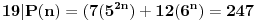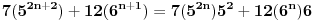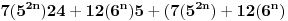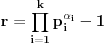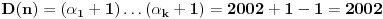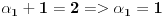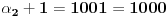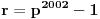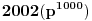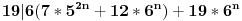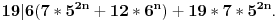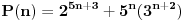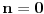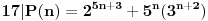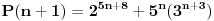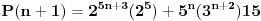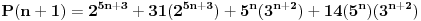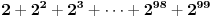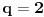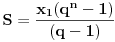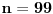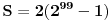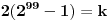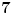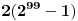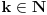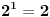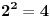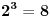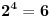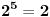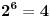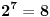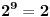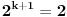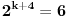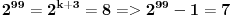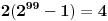|
|
[ Viktor84 @ 12.06.2011. 17:43 ] @
|
| Ovako imam velik problem sa teoriju brojeva i evo nekoliko zadataka ako neko moze da mi pomogne da razberem sustinu oko nacina za resenje ovih zadatka,hvala unapred na svakoga ko moze da pomogne.Znaci:
Priva zadaca:
1.Dokazi da 19|(7*5^(2*n)+12*6^n),za svaki npripada na N mnozestvo;
2.Dokazi da ako P je prost broj,(p^2002)-1 je slozen.
3.Dokazi da 17|(2^(5n+3)+(5^n)*3^(n+2)),za svaki pozitivan broj iz N mnozestva,
Znaci odelio sam neke brojeve sa zagrada za to sto na primer 5^(2*n) je 5 na 2*n stepen.
Havala unapred na onoga koji moze da mi pomogne ,inace prvi put pisujem na ovaj forum mada cesto ga koristim i ni sam nasao ovakve zadace za da ne bi morao da napisem ja,
Pozdrav. |
[ Sonec @ 12.06.2011. 18:26 ] @
1. Dokazati da je 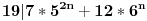 , za svako 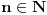 . (ako sam dobro razumeo)
Resenje. Koristi se matematicka indukcija. 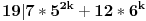
za 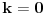 dobija se 19|19, sto je tacno
indukciona hipoteza: za 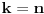 , 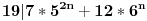
indukcioni korak: 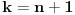 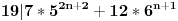
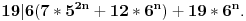
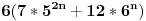 je deljivo sa 19 po indukcionoj hipotezi, a 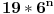 je takodje deljivo sa 19.
pa je i zbir dva broja koja su deljiva sa 19, deljiv sa 19. [ Sonec @ 12.06.2011. 18:38 ] @
2.Dokazati da ako je  prost broj, da je 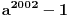 slozen broj.
Resenje. Ovde mozemo iskoristiti Malu Fermaovu teoremu, koja u jednom od svojih oblika glasi:
Terema. Ako je  prost broj i  ceo broj uzajamno prost broj sa  , onda je 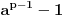 deljivo sa  .
U ovom slucaju,  je 2003, sto je prost broj, a kako je  prost broj, to su ova dva broja uzajamno prosta.
Pa je samim tim broj 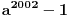 deljiv sa 2003, a samim tim je taj broj i slozen.
P.S verujem da se 3 zadatak radi slicno kao i 1. [ edisnp @ 12.06.2011. 18:39 ] @
1 zadatak: 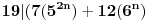 dokazujes indukcijom po 
za  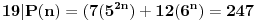 tacno
za n je ispunjeno indukcijska pretpostavka
dokazujes za  i dobijes slijedece: 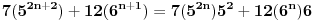
iz toga izdvojis indukcijsku prepostavku 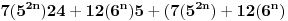 koja je uvek tacna.Dalje mozes nastavit sam.
Za drugi zadatak:  ,
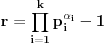 , 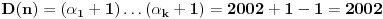
 , 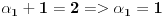 , 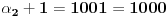 ,  jer je 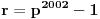 ,Konacno 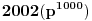 ,sto je slozen broj. [ Viktor84 @ 12.06.2011. 18:40 ] @
Hvala na odgovoru ,kako sto si napisao tako je i bila sastavljena zadaca,
Znaci sad mi se delumno razjasnila posto ni sam nekoi matematicar ne znam od gde si dosao do
19|6(7*5^{2n}+12*6^n) + 19 * 6^n.
Ipak hvala na odogovoru nadam se da ce i za sledeki 2 zadatka neko pomoci..
[ edisnp @ 12.06.2011. 18:44 ] @
@Viktor84 Treci zadatak se radi slicno kao i drugi matematickom indukcijom.
[ Sonec @ 12.06.2011. 18:49 ] @
Napravio sam malu gresku: umesto 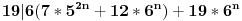 treba da stoji 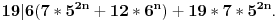
A dalje se radi istom logikom... [ Sonec @ 12.06.2011. 19:11 ] @
Jel ti jasno ?  [ Viktor84 @ 12.06.2011. 20:11 ] @
Hvala vam mnogo sad sam poceo da razumem sa koji princip se resavljaju ove zadatke.
[ edisnp @ 12.06.2011. 20:35 ] @
Evo ti resenje jos ovog treceg zadatka:
1) 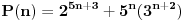 ,za 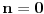 ,  ,sto je tacno.
2) 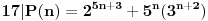 ,indukcijsa pretpostavka.
za ,  , 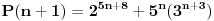
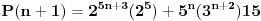
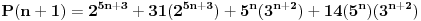

[ Viktor84 @ 12.06.2011. 21:44 ] @
Hvala vam svima koji ste mi pomogli sa ovim zadatcima,spremam ispit pa ako moze pomos za jos jednu zadacu,naizgled je prosta ali nikako da resim ono teoretski ne za resavljanjem kako sto treba.
Zadatak je:
Dokazi da 7 je deljitel na 2+2^2+2^3+2^4+....+2^99;
[ edisnp @ 12.06.2011. 22:40 ] @
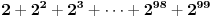 je geometrijski niz.
Geometrijski niz:  i 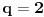 ,
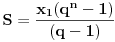 , 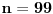 , 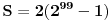 .
Neka ti je 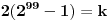
Broj 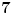 deli broj  ,ako je i neki broj  deljiv sa 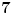 ,
a broj  se dobija tako sto uklonimo cifru jedinica broja  i od toga jos oduzmemo
dvostruku cifru jedinica broja  . [ Viktor84 @ 12.06.2011. 23:12 ] @
Hvala na ulozeni trud ali moram da kazem da sa ovom zadacom nista mi nije jasno , mnogo dela mi fale i nemogu da svatim kako da dokazem.
[ edisnp @ 12.06.2011. 23:34 ] @
Kao prvo bi trebao da nadjes cifru jedinica broja 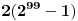 . [ Viktor84 @ 12.06.2011. 23:53 ] @
Ja stvarno se izvinjavljam ja sam iz Makedonije i ovo jedinicu cifru brojevima mislim da kazes -koliko cifre ima u broju znaci sa digitrona nasao sam da
2(2^{99}-1) ima 20 cifre i sada od koj broj x da oduzmem
Da ne nesta loso shvatam nije mi jasno.
[ Sonec @ 12.06.2011. 23:54 ] @
[ edisnp @ 12.06.2011. 23:55 ] @
Ne nego treba da nadjes poslednju cifru broja 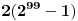 . [ Sonec @ 14.06.2011. 12:51 ] @
edisnp, jel nije problem da dovrsis zadatak...
[ h4su @ 14.06.2011. 12:59 ] @
2^3 kongruentno sa 1 mod 7
2^99=(2^3)^33 kongruentno sa 1^33 tj 1 po modulu 7 prema tome 2^99-1 kongr. sa 0 po mod 7 tj. djeljivo sa 7 i to je to
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|