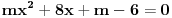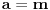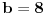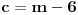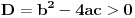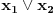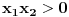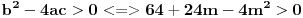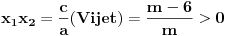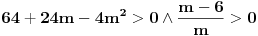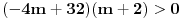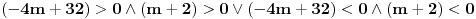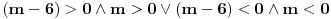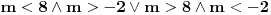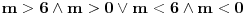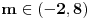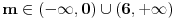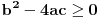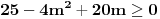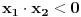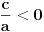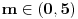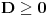[ patkan1992 @ 13.06.2011. 21:14 ] @
|
[ petarm @ 13.06.2011. 21:52 ] @
[ SrdjanR271 @ 13.06.2011. 21:56 ] @
Diskriminanta>0 i x1*x2>0
Pogledaj negde "priroda resenja kv. jednacine" i Vijetove formule Ako nisam pogresio ima dva cela broja m za koje su resenja realna, medjusobno razlicita i istog znaka [ patkan1992 @ 13.06.2011. 22:24 ] @
Dobio sam
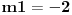 i i 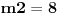 . Jesu to resenja? U resenjima mi pise da je broj resenja: 2 ; i jeste da kad nadjem m1 i m2 dobijem dva resenja, ali nisam siguran da su to ta prava resenja? . Jesu to resenja? U resenjima mi pise da je broj resenja: 2 ; i jeste da kad nadjem m1 i m2 dobijem dva resenja, ali nisam siguran da su to ta prava resenja?Citao sam nesto, ali mi i dalje nije jasno na koji nacin "realna, medjusobno razlicita i istog znaka (oba su pozitivna, ili su oba negativna)" utice na resenja zadatka? [ SrdjanR271 @ 13.06.2011. 22:48 ] @
[ SrdjanR271 @ 13.06.2011. 23:12 ] @
Zaboravio sam to da napomenem.
[ patkan1992 @ 14.06.2011. 01:29 ] @
[ edisnp @ 14.06.2011. 01:43 ] @
[ patkan1992 @ 14.06.2011. 13:23 ] @
[ pitomir @ 14.06.2011. 14:04 ] @
Jednostavno nacrtaj tablicu za obe nejednacine.
[ patkan1992 @ 14.06.2011. 14:51 ] @
Nacrtao sam je. E sad nisam siguran da li na jednoj crti treba da se stavi i 0 ili ne? Posto imam da je
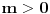 Uradio sam bez 0 i dobijam + samo izmedju 6 i 8, a ako stavim i interval od -2 do 0, dobijam + izmedju -2 i 0, i izmedju 6 i 8 Ako je sa nulom, onda bi resenje bilo: -1 i 7, zar ne? I to bi bila ta dva resenja? [ pitomir @ 14.06.2011. 15:47 ] @
[ patkan1992 @ 14.06.2011. 16:05 ] @
Odakle tebi sada
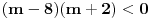 ? Koliko kapiram to ti je iz resenja kv. jedn ? Koliko kapiram to ti je iz resenja kv. jedn 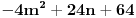 Ali zar ne bi trebalo da bude 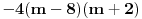 ? I zasto manje od nule, zar ne treba vece? ? I zasto manje od nule, zar ne treba vece?I kako da presecem posle resenja? Nikad mi nisu isle nejednacine, tj. nikad nisam znao da nadjem resenja, da l preko tablice, da l preko brojevne prave. :/ Sad sam skroz zbunjen... :( [ pitomir @ 14.06.2011. 17:20 ] @
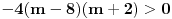 Podelis nejednakost sa -4 i dobijes 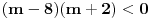 . I to ti je ona tablica sto sam ti okacila u prethodnom postu. Isto vazi i za nejednakost . I to ti je ona tablica sto sam ti okacila u prethodnom postu. Isto vazi i za nejednakost 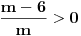 . I nacrtas na istoj brojevnoj pravoj resenja obe nejednacine, vidis gde se seku i u tom intervalu prebrojis cele brojeve. . I nacrtas na istoj brojevnoj pravoj resenja obe nejednacine, vidis gde se seku i u tom intervalu prebrojis cele brojeve.[Ovu poruku je menjao pitomir dana 14.06.2011. u 18:38 GMT+1] [ patkan1992 @ 14.06.2011. 17:49 ] @
Shvatio sam ovaj zadatak, e sad imam problem sa slicnim.
Koliko ima prirodnih brojeva m za koje su resenja kvadratne jednacine 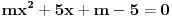 realna i suprotnog znaka? realna i suprotnog znaka?Tu radim sistem od 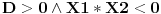 . Jel da? . Jel da?Za m1,2 dobijam: m1= 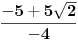 i m2= i m2=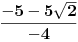 Da l treba ovo da vadim iz korena, tj da izracunam lepo? Ako da - dobijam da je m1 = 0.51, a m2 = 3.01. I ako se 3 uzima za resenje dobijam 3 resenja, ako ne, onda imam dva resenja, a to su 1 i 2. Da l treba ovo da vadim iz korena, tj da izracunam lepo? Ako da - dobijam da je m1 = 0.51, a m2 = 3.01. I ako se 3 uzima za resenje dobijam 3 resenja, ako ne, onda imam dva resenja, a to su 1 i 2.Ja dobijam tu 3 ili 2 (ako se trojka ne racuna) resenja, a treba 4. Ne znam gde gresim... [Ovu poruku je menjao patkan1992 dana 14.06.2011. u 19:17 GMT+1] [Ovu poruku je menjao patkan1992 dana 14.06.2011. u 19:18 GMT+1] [Ovu poruku je menjao patkan1992 dana 14.06.2011. u 19:19 GMT+1] [ petarm @ 14.06.2011. 18:16 ] @
Koren
\sqrt{} Razlomak \frac{}{} [ pitomir @ 14.06.2011. 18:18 ] @
[ patkan1992 @ 14.06.2011. 18:29 ] @
[ SrdjanR271 @ 14.06.2011. 20:16 ] @
Da. Procitaj Vijetove formule i prirodu rešenja kv. jednačine.
[ edisnp @ 14.06.2011. 20:21 ] @
Evo pogledaj ovo:http://www.matematiranje.com/II%20godina/vietove_formule.pdf.
[ patkan1992 @ 14.06.2011. 21:12 ] @
Hvala puno svima! Sad mi je jasno ovo :)
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|