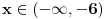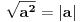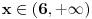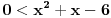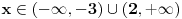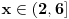[ patkan1992 @ 14.06.2011. 22:04 ] @
|
[ edisnp @ 14.06.2011. 22:23 ] @
[ SrdjanR271 @ 14.06.2011. 22:40 ] @
[ patkan1992 @ 14.06.2011. 22:41 ] @
A znaci nije nepravilno promeniti strane?
Ako promenim tako strane, zar ne pomogu raditi po ovome 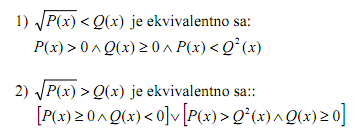 ? ?A ako mora da se radi ovako kako si rekao, nije mi jasno zbog cega ostaje  kada se kvadrira leva strana? Zasto ne ostane samo kada se kvadrira leva strana? Zasto ne ostane samo 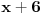 ? ?EDIT: Srdjane, pogledao sam to, ali kao sto sam naveo u naslovu - buni me sto je koren sa desne strane.... [ patkan1992 @ 14.06.2011. 22:58 ] @
@edisnp,
Ako koren stavim na levu stranu, mogu li da resim ovu nejednacinu upotrebom ekvivalencija? [ edisnp @ 14.06.2011. 23:07 ] @
Sto ne bi mogo
[ Sonec @ 15.06.2011. 00:13 ] @
[ patkan1992 @ 15.06.2011. 00:24 ] @
Sonec,
Mogu li je resiti upotrebom ovih ekvivalencija 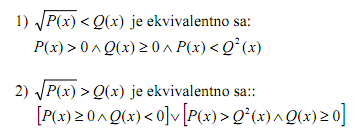 ? ?Nisam siguran da li je pravino to sto menjam strane da bi koren stavio na levu stranu....? A kad ga stavim na levu stranu mislim da bi trebalo da vaze ove ekvivalencije sa slike iznad, zar ne? [ Sonec @ 15.06.2011. 00:28 ] @
Da li ti napisao Pera > Djura ili Djura < Pera, svejedno je...
tako, da, odgovor je DA, naravno da mozes... A bas se te ekvivalencije, cini mi se, i koriste. [ patkan1992 @ 15.06.2011. 00:50 ] @
[ Sonec @ 15.06.2011. 13:04 ] @
[ patkan1992 @ 15.06.2011. 13:55 ] @
Nemoguce, posto ima 4 resenja. Ja sam dobio da su resenja
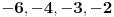 Dobijam da je 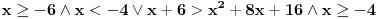 Kada resim ovu kvadratnu jednacinu dobijam da su resenja 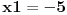 i i 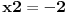 . Odatle uzimam interval . Odatle uzimam interval 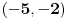 . I znaci dobijam da . I znaci dobijam da 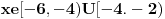 . .I kada sve to "spakujem" na brojevnoj pravi dobijam da su resenj: 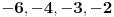 . .Moguce da gresim, ali meni se ovo kako sam uradio cini kao ispravno. Mada si me sada zbunio ovim praznim skupom.... Skroz mi je nejasno kako se gledaju resenja nejednacina na brojevnoj pravi, ako mozes da mi objasnis malo to kako bih lakse shvatio? [ Sonec @ 15.06.2011. 14:02 ] @
[ patkan1992 @ 15.06.2011. 14:12 ] @
Ja mislim da ne...
Kako sam ja dobio, ispada: 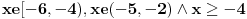 Ali opet kazem nisam siguran, ne znam da gledam to gde i kako x pripada. :/ EDIT: Citat: Aham ok... Hvala, razumeo sam. :) A mozes li mi reci, ako imam da je manjejednako manjejednako sta je tu presek resenja (celi brojevi)? Da li i ili i ? (Nisam znao da stavim znak manjejednako, pa se nadam da shvatas.) Ako te ovo sto sam citirao buni: To nema veze sa ovim zadatkom... Ovo se odnosi na zadatak: 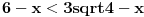 To sam samo pitao jer mi nije jasno kako se gleda presek svih resenja.... Nikako ne kapiram.. [ Sonec @ 15.06.2011. 14:17 ] @
Da li je ovo
Citat: patkan1992: A mozes li mi reci, ako imam da je  manjejednako manjejednako 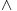 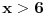 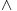  manjejednako manjejednako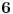 sta je tu presek resenja (celi brojevi)? Da li sta je tu presek resenja (celi brojevi)? Da li  i i  ili ili  i i 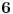 ? ?(Nisam znao da stavim znak manjejednako, pa se nadam da shvatas.) u stvari ovo To te ja pitam. [ patkan1992 @ 15.06.2011. 14:24 ] @
[ Sonec @ 15.06.2011. 14:33 ] @
Aj mi napisi zadatak koji resavas, ja cu resiti i obrazlozicu resenje.
[ patkan1992 @ 15.06.2011. 14:43 ] @
[ Sonec @ 15.06.2011. 15:12 ] @
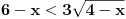  zatim, koristis one uslove (ekvivalencije) koje si gore naveo... 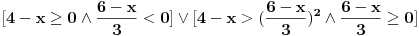 Resenje prve uglaste zagrade [...] je prazan skup, jer je 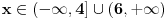 , a to je prazan skup (ako ne znas preko brojevne prave, ajde logicki, , a to je prazan skup (ako ne znas preko brojevne prave, ajde logicki,  treba da je manje ili jednako od 4, a istovremeno vece od 6, pa ne postoji takvo treba da je manje ili jednako od 4, a istovremeno vece od 6, pa ne postoji takvo  koje zadovoljava ove osobine) koje zadovoljava ove osobine)Resenje druge uglaste zagrade [...] je  , jer je resenje , jer je resenje   , a , a 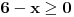 je je 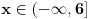 , a presek ova dva skupa je , a presek ova dva skupa je  I sad, imas da  pripada praznom skupu ili pripada praznom skupu ili  , tj. uniju ova 2 skupa, pa je konacno resenje , tj. uniju ova 2 skupa, pa je konacno resenje  , kako ti trazis celobrojna resenja, to su onda 1 i 2. , kako ti trazis celobrojna resenja, to su onda 1 i 2.Sad cu i resenje 2 zadatka, samo dok otkucam... [ patkan1992 @ 15.06.2011. 15:23 ] @
[ Sonec @ 15.06.2011. 15:33 ] @
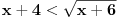 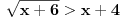 ponovo, pomocu onih ekvivalencija imamo: 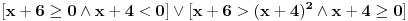 Resenje prve uglaste zagrade [...] je 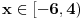 (to valjda znas zbog cega je...) (to valjda znas zbog cega je...)Resenje druge zagrade [...] je  , jer je resenje , jer je resenje  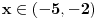 , a resenje , a resenje 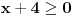 je je  , a tebi treba presek ova dva resenja (za resenje druge zagrade [...]),a to je , a tebi treba presek ova dva resenja (za resenje druge zagrade [...]),a to je  Za konacno resenje se uzima unija (jer izmedju zagrada [...] stoji ILI, tj. unija), pa odatle sledi  , a to je samo , a to je samo 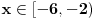 A posto trazis celobrojna resenja, resenja su -6,-5,-4,-3 [ Sonec @ 15.06.2011. 15:36 ] @
Inace, pogledaj link koji ti je Srdjan dao, http://www.matematiranje.com/I...na/iracionalne_nejednacine.pdf, imas tu kompletno uradjene slicne zadatke (sa presecima intervala, sto vidim da tebe zbunjuje malo...)
[ patkan1992 @ 15.06.2011. 15:57 ] @
Bolje nije moglo da bude objasnjeno.. Hvala ti najvise!
Mozes li da mi kazes sta dobijas za ovaj: 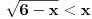 ? ?Imam sledece: 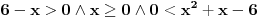 - Za ovu kvadratnu dobijam: - Za ovu kvadratnu dobijam: 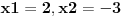 , pa odatle imam , pa odatle imam  . .I ja kao resenje dobijam:  . A u resenjima pise da je resenje: . A u resenjima pise da je resenje:  Nigde nemam da je  manjejednako manjejednako 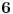 , vec samo , vec samo 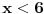 . A imam . A imam  , pa odatle mi da se i broj 2 racuna. , pa odatle mi da se i broj 2 racuna.[ Sonec @ 15.06.2011. 16:38 ] @
[ patkan1992 @ 15.06.2011. 19:32 ] @
Kako da naprave takvu gresku :/
Hvala puno, sada mi je mnogo jasnije ovo! :) [ SrdjanR271 @ 15.06.2011. 22:06 ] @
[url=http://www.google.com/url?sa=t&source=web&cd=13&ved=0CCEQFjACOAo&url=http%3A%2F%2Fwww.prilika.net%2Firacnejed1.p...VC4ssLIMDq54j5Yzjw&cad=rja]Iracionalne ne j-ne[/url]
[ SrdjanR271 @ 15.06.2011. 22:08 ] @
[ ana0201 @ 19.01.2012. 11:49 ] @
Moze li mi neko pomoci oko ovog zadatka? pod velikim korenom je Xna kv.-5x+4<x-3
Hvala unapred... [ Nedeljko @ 19.01.2012. 12:28 ] @
Obzirom da je kvadratni koren nenegativna funkcija, desna strana mora biti veća od nule, tj. x>3. Takođe, potkorena veličina mora biti nenegativna. E, onda kada su obe strane definisane i nenegativne, kvadriraj nejednačinu i dodaj dobijeni uslov.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|