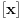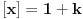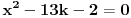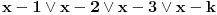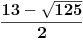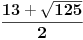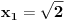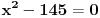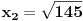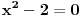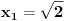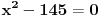[ Nuh @ 15.06.2011. 16:44 ] @
|
[ Sherlock Holmes @ 15.06.2011. 17:59 ] @
Ako je [x] najveci ceo broj ne veci od x, onda mozemo da napisemo sledece [x]=x-1. I to zamenis. Nisam 100% siguran, ali probaj tako da uradis.
[ edisnp @ 15.06.2011. 18:08 ] @
[ Nuh @ 15.06.2011. 19:33 ] @
Moze li neko da mi pomogne kako da resim jednacinu.
[ Sherlock Holmes @ 15.06.2011. 20:14 ] @
Ali pise da je NAJVECI ceo broj, ne veci od X. Ako napises x-2 znaci da ima od njega veci ceo broj koji je manji od x a to je x-1. Mozda gresim.
[ miki069 @ 16.06.2011. 08:39 ] @
X ne mora biti ceo broj.
[X] je oznaka za ceo deo od X. [2.78] = 2 [4] = 4 [5.99999] = 5 [-1.87] = -2 [X] = k gde važe nejednakosti: X-1 < k <= X [ djoka_l @ 16.06.2011. 09:13 ] @
[ Nuh @ 16.06.2011. 14:31 ] @
[ miki069 @ 16.06.2011. 14:51 ] @
X2=12.090169943749474241022934171828
[12.090169943749474241022934171828] = 12 To je zameniu u početne jednačine umesto [X]. X2 jeste veći od 12, ali X1 nije veći od 1, nego je manji od 1. Međutim, opet je dobio ispravna rešenja. Obična kvadratna jednačina mu je samo služila da locira X. [ djoka_l @ 16.06.2011. 22:23 ] @
Evo još malo da objasnim.
Početna jednačina se posebno rešava na poluzatvorenim intervalima [k, k+1) gde je k ceo broj ( 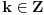 ). ).Za 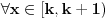 važi važi 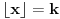 , pa jednačina , pa jednačina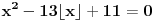 može da se napiše kao 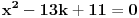 za za 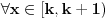 Za 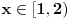 jednčina glasi 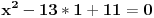 , , a kada se to sredi, ostane 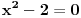 Ova jednačina ima dva realna korena 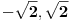 , ali samo rešenje , ali samo rešenje 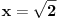 pripada intervalu [1,2). pripada intervalu [1,2).Odmah da kažem da sam i ja napravio grešku, jednačina ima 4 rešenja (ja sam ti dao samo dva). Evo kako Wolfram alpha to lepo reši: [url=http://www.wolframalpha.com/input/?i=x^2-13int%28x%29%2B11%3D0]Wolfram Alpha[/url] Uf, ES ne ume da prikaže link kako treba, idi na sajt http://www.wolframalpha.com i ukucaj: x^2-13int(x)+11=0 [ Nedeljko @ 17.07.2011. 12:17 ] @
Pošto me je jedan član zamolio, hajde da priložim svoje rešenje.
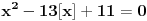 , ,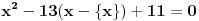 , ,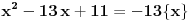 . .Odavde sledi da je 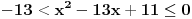 . .Rešenje poslednje dvostruke nejednačine je 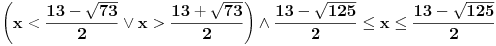 , ,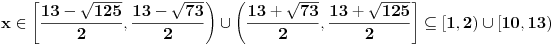 . .Za 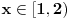 jednačina se svodi na jednačina se svodi na 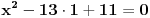 , čije je jedino rešenje u skupu , čije je jedino rešenje u skupu 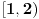 dato sa dato sa 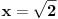 . .Za 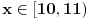 jednačina se svodi na jednačina se svodi na 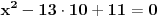 , čije je jedino rešenje u skupu , čije je jedino rešenje u skupu 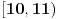 dato sa dato sa 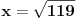 . .Za 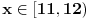 jednačina se svodi na jednačina se svodi na 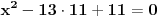 , čije je jedino rešenje u skupu , čije je jedino rešenje u skupu 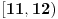 dato sa dato sa 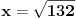 . .Za 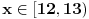 jednačina se svodi na jednačina se svodi na 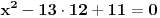 , čije je jedino rešenje u skupu , čije je jedino rešenje u skupu 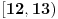 dato sa dato sa 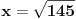 . .Dakle, jednačina ima četiri rešenja. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|