[ vladadada @ 20.06.2011. 14:15 ] @
Naci minimalne i maksimalne vrednosti funkcije:

y= x^5 - 5x^4 + 5x^3 + 1 , za X element [-1,2]

Moj rezon:
Nadjem prvi izvod funkcije, odnosno y' = 5x^4 -20x^3 +15x^2
Izjadnacim prvi izvod sa nulom 0 = 5x^2(x-1)(x-3) i dobijem 3 nule x1=0, x2=1 i x3=3
Pomocu tablice vidim da je izvod pozitivan u intervalu (-beskonacno, 1)U(3,beskonacno) a da je negativan u intervalu (1,3) sto znaci da ima y(max) za x=1 i y(min) za x=3 ali ovaj y(min) odbacujem zbog uslova zadatka da je X element [-1,2]
Uvrstim x=1 u pocetnu funkciju i dobijem da je y(max)=2 sto je tacno resenje medjutim oni imaju i y(min)= -10 za x= -1 pa ako bi neko mogao da mi objasni odakle to?

Ovaj zadatak ima pod a), b), c) i d), pod a) i d) ima interval i u oba zadatka dobijem polovicno resenje a pod b) i c) nema intervala i dobijem potpuno resenje.


Hvala unapred!
[ djoka_l @ 20.06.2011. 14:34 ] @
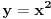
Pa ne mora da bude izvod funkcije nula u tački koja pripada nekom intervalu, da bi u toj tački funkcija imala minimum ili maksimum. Uzmi na primer na intervalu [-1,-1/2]. Maksimum te funkcije je za x=-1, minimum za x=-1/2, dok je prvi izvod funkcije jednak nuli za x=0 i ne nalazi se u posmatranom intervalu...
Osim lokalnog minimuma ili maksimuma, izvod može biti 0 i u prevojnim tačkama (ako ih ima). Da bi našao min-max na intervalu, obavezno proveri koje su vrednosti f-je na granicama intervala.
[ Janinka @ 20.06.2011. 14:40 ] @
Koliko sam ja shvatila, zadatak je: Naci minimalne i maksimalne vrednosti date funkcije u intervalu [-1,2].
Jedina logika u resenju je, da se proverri vrednost funkcije u krajevima intervala,koji pripadaju intervalu, pa posto je
f(-1)=-10, f(2)=-7, a u datom intervalu je f(1)=2,(to je max), znaci da je minimalna vrednost funkcije u datom intervalu
f(-1)=-10, jer je -10<-7 ( iako to nije tacka ekstrema, posto je minimum date funkcije f(3)=-26) .

[ vladadada @ 20.06.2011. 17:01 ] @
Hvala na brzom odgovoru :)
[ Sini82 @ 21.06.2011. 17:05 ] @
Ispitaj osobine i skiciraj grafik funkcije.