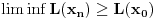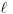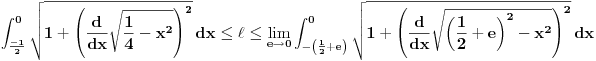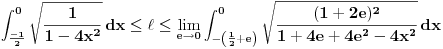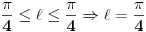|
|
[ marinowski @ 23.06.2011. 19:25 ] @
|
| Brat mi je postavio interesantan zadatak, obojica smo matematičari. Jednom njegovom prijatelju, gimnazijskom profesoru, na zadnjem času je učenik postavio interesantan zadatak. Profesor je bio zbunjen i rekao da će razmisliti preko leta.
Evo i zadatka:
Imamo kvadrat stranice dužine jedan. Obim je četiri. Upisana je kružnica, kojoj je, jel ... obim Pi.
E sada, presavijemo četiri ugla kvadrata tako da dodiruju kružnicu. Ako nije jasno, onda možemo i ovako: isečemo četiri kvadrata iz uglova tako da dodiruju kružnicu. Pošto novi oblik izgleda kao da smo "presavili" uglove, obim je, očito, opet četiri. Nastavljamo i dalje postupak, presavijamo, isecamo, whatever, i obim je uvek četiri, a novi oblik koji je opisan oko kružnice sve bolje i bolje aproksimira kružnicu.
Nastavimo to ... u beskonačnost.
Pitanje je: zašto onda Pi nije jednako četiri, pošto je obim uvek četiri?
Odgovor je na prvi pogled jednostavan, znamo da nije, i beskonačnost je mnogo zeznutija nego ono što možemo zamisliti dok razmišljamo makar o vrlo dalekoj konačnosti ... imam jednu ideju, prijatelj ima jednu drugu, da čujem vas :)
|
[ Sherlock Holmes @ 23.06.2011. 19:54 ] @
Meni nije jasno, kako presavijas kvadrat, tj. polovis uglove?
[ edisnp @ 23.06.2011. 20:02 ] @
Cekaj jel presavijas il isecas uglove ako ih isecas onda obim kvadrata nije vise jednak  .
Pojasni malo. [ Bojan Basic @ 23.06.2011. 20:10 ] @
Citat: marinowski:
Odgovor je na prvi pogled jednostavan, znamo da nije, i beskonačnost je mnogo zeznutija nego ono što možemo zamisliti dok razmišljamo makar o vrlo dalekoj konačnosti ... imam jednu ideju, prijatelj ima jednu drugu, da čujem vas :)
Najjednostavnije objašnjenje je da problem leži u tome što konvergencija, čak ni uniformna konvergencija, ne očuvava dužinu krive. [ VlaK @ 23.06.2011. 20:24 ] @
Citat: edisnp: Cekaj jel presavijas il isecas uglove ako ih isecas onda obim kvadrata nije vise jednak  .
Pojasni malo.
Jel ovako?
 [ marinowski @ 23.06.2011. 20:31 ] @
Obim presavijenog kvadrata ostaje četiri.
Zamislite da uzmete uglove kvadrata i da ih povučete tako da dotiču kružnicu, a da je ono što nedostaje kvadrat ...
Ako nije jasno, nacrtaću :)
//
Bojane, izgleda da si u pravu. Da li to može jednostanije da se objasni, a da se ne koristi teška artiljerija? : )
[ marinowski @ 23.06.2011. 20:34 ] @
@VlaK: Da, da, baš tako ...
Meni je interesantno pitanje da li se ovo može obrazložiti ne koristeći visokoškolsku matematiku, pošto je pitanje postavio (doduše itekako nadareni) srednjoškolac.
[ berazorica @ 24.06.2011. 06:42 ] @
Nije baš teška artiljerija i visokoškolska matematika ako se konstatuje šta je to što konvergira: niz površina figura nastalih na opisani način konvergira ka površini kruga. Što se obima tiče, i osnovcu se može objasniti da je on konstantan.
[ marinowski @ 24.06.2011. 07:54 ] @
Ovde se ne radi o površinama, nego o obimu.
Dakle, pitanje je: kako je moguće ako je obim figure konstantan (4), a da on konvergira obimu kružnice (Pi).
Iskreno, nisam još dobio odgovor koji bi me *potpuno* uverio u rešenje. A naročito zato što su odgovori bili kontradiktorni :)
[ Chobicus @ 24.06.2011. 08:49 ] @
Sličan problem sam imao u glavi kao klinac.
Posmatrao sam pravougli trougao čija je hipotenuza "stepenasta" tj. sastoji se od beskonačno mnogo "stepenika". Zbir dužina horizontalnog dela stepenika je jednak dužini horizontalne katete a zbir dužina vertikalnih stepenika je jednak dužini vertikalne katete.
Zašto usitnjavanjem ovih "stepenika" dužina hipotenuze ne postane jednaka biru dužina dve katete? :)
[ berazorica @ 24.06.2011. 09:44 ] @
Citat: marinowski: Ovde se ne radi o površinama, nego o obimu.
Dakle, pitanje je: kako je moguće ako je obim figure konstantan (4), a da on konvergira obimu kružnice (Pi).
Iskreno, nisam još dobio odgovor koji bi me *potpuno* uverio u rešenje. A naročito zato što su odgovori bili kontradiktorni :)
Obimi figura predstavljaju konstantan niz koji NE konvergira obimu kružnice! Po kom kriterijumu misliš da konvergira? Po tome što površina koju ograničava ta izlomljena kriva linija konvergira?
Dakle, ako odsecaš "kvadratiće", odbacuješ delove površine 4 i to (površine koje se smanjuju) konvergira ka površini kruga, a ako figuru oblika kvadrata (model od žice npr.) preoblikuješ u neku drugu izlomljenu liniju, time ne menjaš njenu dužinu. U stvari, transliraš delove linije (pri čemu ne dolazi do poklapanja slika pojedinih delova), pa im ne menjaš dužinu, a ni ukupnu dužinu izlomljene linije.
Pitanje: zašto obim figure ne konvergira ka Pi?
Odgovor: zato što je translacija transformacija podudarnosti. [ miki069 @ 24.06.2011. 09:53 ] @
Razlika obima kvadrata i kruga je 4-Pi i ona je konstantna koliko god usitnjavao "viškove" od kvadrata.
Obim "viškova" teži ka nuli, ali nikada nije nula. Ujedno broj nazubljenih "viškova" teži ka beskonačnosti.
0*beskonačno je neodređen oblik granične vrednosti. Može biti 0, beskonačnoo ili neka const<>0.
Pošto je usaglašena brzina padanja obima "viškova" ka 0 i povećavanja broja zubaca "viškova", taj limes daje konstantu <> 0.
Ovde je ta konstanta tačno = 4-pi.
Po toj logici Ahil nikada ne bi stigao kornjaču, iako je 10* brži od nje.
[ marinowski @ 24.06.2011. 09:57 ] @
Čak ni ako stvari odu u beskonačnost? Kao što rekoh, beskonačnost nije uvek zdravorazumska na prvi pogled.
Prijatelj mi je napomenuo baš to, da će ovaj oblik više konvergirati nečemu fraktalnom, obliku kao kochova pahuljica, a ne kružnici.
Evo kako ide moje razmišljanje, mislim da mi je lakše objasniti na Chobicusovom primeru:
napravi se funkcija koja će određivati dužinu prelomljenog delića u odnosu na iteraciju. onda je dužina aproksimirane hipotenuze broj delića puta dužina delića (koji je konstantan i iznosi zbiru kateta u konačnom slučaju).
Kada se to pusti u beskonačnost, onda dužina delića idu u nulu, a broj delića u beskonačnost, a nula puta beskonačno je neodređen izraz. Ako nađemo limes toga, trebalo bi da dobijemo dužinu hipotenuze, ili u inicijalnom zadatku, obim kružnice, Pi.
Ispravite me ako grešim.
[ Bojan Basic @ 24.06.2011. 14:00 ] @
Citat: marinowski:
Prijatelj mi je napomenuo baš to, da će ovaj oblik više konvergirati nečemu fraktalnom, obliku kao kochova pahuljica, a ne kružnici.
Neće, ovaj oblik zaista konvergira ka kružnici, i ta konvergencija je čak uniformna. Problem je prosto u tome što, kao što rekoh, uniformna konvergencija ne očuvava dužinu (tj., ako niz krivih uniformno konvergira ka nekoj graničnoj krivoj, dužina granične krive nije nužno jednaka limesu dužina krivih koje konvergiraju ka njoj).
Kako to objasniti srednjoškolcu a bez pomena konvergencije? Teško, pošto je konvergencija već sadržana u pitanju — to što si napisao u prvoj poruci: „Nastavimo to ... u beskonačnost“ upravo iz znači „Posmatrajmo krivu koja je granična vrednost ovakvog niza“. Najbolje objašnjenje koje mogu ponuditi za sredjoškolca je ovako nešto: „Taj poslednji korak koji pravimo, kada sve bolje i bolje aproksimacije kružnice na kraju poistovetimo sa samom kružnicom, ima svoj precizan matematički opis. Bitno je da se time neke osobine koje su ove usputne aproksimacije imale očuvavaju, ali ima i osobina koje se ne moraju očuvavati. Dužina je tu jedna osobina koja se ne očuvava, i to objašnjava zašto dužina (obim) kružnice nije jednaka dužini (obimu) zajedničkoj za sve ove aproksimacije.“ [ marinowski @ 24.06.2011. 14:41 ] @
Bojane, imaš neki link koji potvrđuje ovo što kažeš? To da konvergencija ne očuvava dužinu.
Nije da ti ne verujem, ali ipak ... dobro je znati :)
[ Bojan Basic @ 24.06.2011. 15:39 ] @
Nisam sad siguran kakav link hoćeš. Da uniformna konvergencija ne očuvava dužinu može se utvrditi bilo kojim kontraprimerom, a takvih samo na ovoj temi postoje dva (tvoj, polazni — i Chobicusov, s pravouglim trouglom). Ti ne bi eksplicitne kontraprimere, nego link gde crno na belo piše „Uniformna konvergencija ne očuvava dužinu“, jesam li dobro razumeo? OK, evo jednog rada gde se proverava šta sve dodatno mora važiti pa da bi konvergencija zaista čuvala dužinu: http://www.ams.org/journals/bu...-6/S0002-9904-1948-09034-6.pdf, i odmah u uvodu stoji:
Citat: Uniform convergence on  of the components 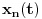 , 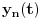 , 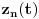 to 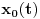 , 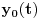 , 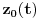 respectively implies only that 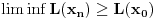 . [ milanche @ 24.06.2011. 15:41 ] @
Malo sam se (iz ciste pasije za resavanjem problema) bacio u razmisljanje - problem je 'bombonica' za mozak.
Iako nisam matematicar, dozvolicu sebi da vam se kao 'komsijin mali kog su pustili da gleda' umesam u diskusiju:
Proces 'uvrtanja usiju' kvadratima ne ocuvava obim kvadrata.
Zapravo, ocuvava ga sve dotle dokle razlicite 'uvrnute usi' nemaju zajednicku ivicu.
Onog momenta kad 'uvrnuto uvo'[k] ima zajednicku ivicu sa 'uvrnutim uvom'[m] - ta zajednicka ivica nestaje, i
obim gubi na vrednosti najmanje za tacan iznos X (a moze da izgubi i vise).
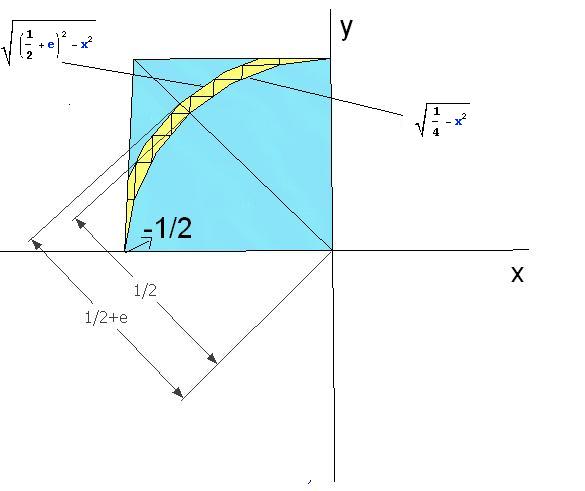
Pogledajte sliku koju sam attach-ovao.
Iako ne odgovara konkretnom problemu (priblizavanje kruznici), ilustruje pojavu gubitka zajednicke ivice. Da bi
bolje ilustrovao lossy process, doveo sam stvari do ekstrema, praveci dva uzastopna 'uvrtanja usiju' kvadrata, u
kojem gubitak ivice oznacene sa 'x' doprinosi padu vrednosti obima za 3x (jer je donji desni polu-kvadrat otisao).
Na srednjoj slicici, obim figure je ocuvan. Na poslednjoj, medjutim, usled efektivnog nestanka ivice 'x' doslo je
do smanjenja vrednosti obima.
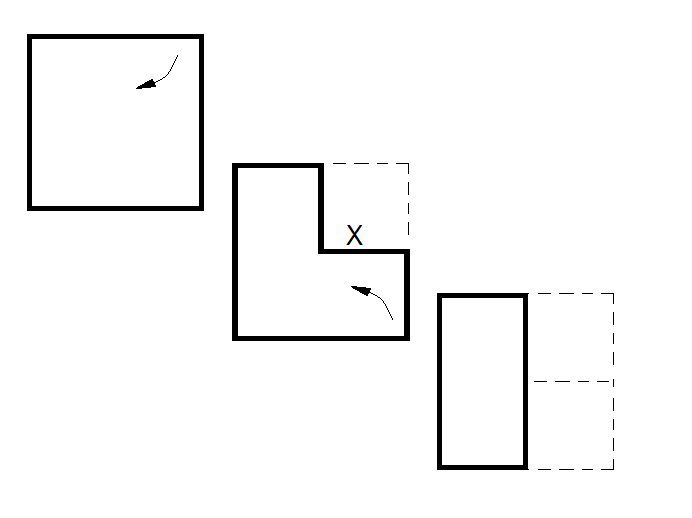
Slicno se desava i kad se pazi da se pridje upisanoj kruznici, samo su gubici, naravno, manji. [ Odin D. @ 24.06.2011. 15:41 ] @
Problem je intuitivno jasan sam po sebi.
Zabuna nastaje uslijed makroskopskog posmatranja pojave. Medjutim, koliko god sitno nazubljivali tu krivu, ona je i dalje "zubata pod mikroskopom", iako "iz daljine" izgleda glatka.
Elem, na ovom crtezu - put od tacke A do tacke B je iste duzine bez obzira koliko ga sitno ili krupno nazubljivali. Horizontalna i vertikalna komponenta puta ostaju uvijek iste.
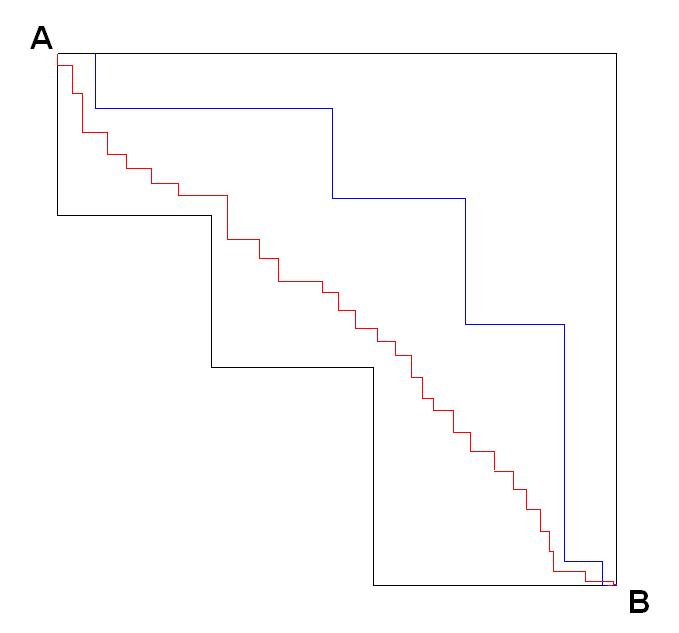
Sa druge strane, ono drugo sto je pomenuo - da se ti trouglovi odsjecaju tetivno od kruga (umjesto da se coskovi zavrcu) - dovelo bi da obim tog poligona dobijenog odsjecanjem coskova tezi obimu kruga.
[ SrdjanR271 @ 24.06.2011. 18:42 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|