Totalno je nebitno sta je bilo posto rulet ne pamti. Ako je npr. bilo deset crvenih za redom, sansa da opet bude crveno je i dalje 50% (ne racunam nulu radi jednostavnijeg objasnjenja).

Slazem se da su podjednake sanse za svaki broj, ali ipak na vise bacanja trebalo bi da budu ispostovani neki zakoni verovatnoce... Makar ja tako mislim ali bi ipak voleo da se javi neko od matematicara.

Samo ako je tih vise bacanja u buducnosti (to i kazu zakoni verovatnoce).

n=log(31/37)/log(0.01)=26
(ako sam razumio šta hoćeš-)

Imaš 99% šansu da će jedan od tih šest brojeva izaći u 26 bacanja.

Kako?

Šansa da neće izaći u prvom bacanju niti jedan od odabranih brojeva je 31/37.
Da neće izaći niti iz dva bacanja je (31/37)^2,a da neće izaći iz n bacanja je (31/37)^n.
Ako želimo da imamo šansu 99% da izađe neki od odabranih ,onda je šansa da neće izaći 0.01.
Treba naći n ako je (31/37)^n=0.01

Upravo tako. Rulet ne pamti istoriju. Pogrešno je uverenje da ako dvojka nije pala u prethodnih 1000 bacanja, da će sada "trebati da počne da se javlja da bi stigla prosek".

Naravno, ne mora da znaci... postoji samo verovatnoca da ce pasti. A ta verovatnoca je sa svakim bacanjem sve veca, ali nikad nece dostici 100%. Stvarno izvuceni brojevi na pravim ruletima pokazuju ucestalost izvlacenja... Recimo na 1000 bacanja neki padnu vise, neki manje ali njihov broj tezi da se izjednaci. Npr. odnos crvena-crna, par-nepar je jako izjednacen...

Hvala zzzz, ta formula mi je bila potrebna.

Verovatnoća neće biti "sve veća i veća".
Verovatnoća da padne broj 19 je 1/37 ili ti nešta manje od 3%, u svakom bacanju.
Ne zavisi od toga koliko puta je pre puta bacano i koliko puta je pao broj 19.
Svako bacanje je nezavisno za sebe.
Uslovna verovatnoća događaja A = pada broj 19, ako se veće desio događaj B = 19 je pao u
predhodnih 1000 puta zaredom, je i dalje 1/37.
Nema nikakvog sistema.

Nije mi jasno šta ti pomaže Milanova formula?
Pokrivaš 6 brojeva u 25 bacanja i pukneš 25*6 = 150 čipova.
Onda dobiješ dobitak od 36 čipova.
Imaš gubitak od 114 čipova.
Možda ga dobiješ i ranije/kasnije sa manjim/većim gubitkom/dobitkom.

Miladine, ta formula koju ti je zzzz dao je za slucaj da su sva bacanja u buducnosti.

Baš tako u budućnosti, za svih 26 bacanja u celini.

Već bilo više puta na ovom forumu, al ajde ponovo:
Ako bacamo 10 puta uzastopno novčić (p pismo, g glava) , podjednako su verovatni sledecih 1024 ishoda:

1. pppppppppp
2. pppppppppg
3. ppppppppgp
4. ppppppppgg
5. pppppppgpp
6. pppppppgpg
7. pppppppggp
8. pppppppggg
.
.
1023. gggggggggp
1024. gggggggggg

Sa verovatnoćama 1/1024.


Ako posle 9 bacanja imas ishod "ppppppppp" (9 pisama), Bajesova formula uslovna verovatnoce kaze da su podjednako verovatne samo 2 preostale moguće hipoteze:

1. pppppppppp
2. pppppppppg

sa verovatnocama po 50%. Ona iskljucuje ostalih 1022 hitpoteza. To je uslovna verovatnoca.
Dakle u desetom bacanju pada p ili g sa istim verovartnoćama od 50% za p i 50% za g.
Nema veze što je već palo svih devet pisama.

Dakle verovatnoća pojave pisma u svakom narednom bacanju je 50% jer se radi o nezavisnim bacanjima.

Ne, broj crvenih i broj crnih ne teže da se izjednače. Štaviše, apsolutna vrednost razlike broja crvenih i broja crnih će težiti beskonačnosti. Odnos broja crvenih i broja crnih će težiti jedinici. To je zato što će broj izvlačenja rasti brže od apsolutne vrednosti razlike. Ako je veliki broj, očekuj da će nakon izvlačenja apsolutna vrednost razlike broja crvenih i broja crnih biti oko 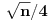. Recimo, posle oko 1,000,000 izvlačenja će razlika biti oko 250, a posle 100,000,000 izvlačenja oko 2,500. Neće se smanjivati, nego povećavati, ali će u poređenju sa brojem izvlačenja biti sve zanemarljivija.

Verovatnoća da u n-tom bacanju padne pismo ako je u prvih n-1 puta palo pismo je

p(A_n|A₁A₂...A_n-1) = p(A₁A₂...A_n)/p(A₁A₂...A_n-1) = (1/2)ⁿ/(1/2)^n-1 = 1/2

Ali možda pokretač teme ima na umu neispravnost mašine i pokušava da proveri da li mašina zaista izbacuje brojeve uniformno. U tom slučaju nisu isključene šanse na dobitak.

Očigledno mešaš pojmove ravnomernosti i nezavisnosti.

O, jel? Gde to?

Sad ste me pokolebali.... da li uopste matematicka verovatnoca moze da se primeni na ovakve slucajeve ili je to cisto samo teorija?
Ja ne znam matematiku ali meni je logicno da ako svaki broj ima istu sansu, cini mi se da posle nekog vremena ipak mora da dodje svaki. Ok ne moze se reci kada ali u praksi recimo svaki broj izadje makar jednom u otprilike 200 bacanja. Cesto i mnogo ranije. Ja to gledam kao recimo igras ruski rulet... pa aj usudi se igraj malo duze, jednom ce da opali...

Pogotovo sto razmatram sektor od nekoliko vezanih brojeva.. cini mi se da je jos veca sansa da povremeno tu ubaci nego da se hvataju brojevi nasumicno rasporedjeni po tocku.

Razmatram fer rulet, znaci bez gresaka i namestanja, iako bas ne verujem u to ali to sad nije tema...

Nezavisnost izvlačenja znači nezavisnost od istorije. To nema veze sa ravnomernošću ishoda (da su svi jednakoverovatni).

Miladine,

Da, može matematička verovatnoća da se primeni, ali teorija verovatnoće nije ono što ti zamišljaš, već ono što piše u odgovarajućim knjigama. Sve što sam napisao je na osnovu teorije verovatnoće.

^Nedeljko

A gde sam ja pobijao ili tvrdio da "Nezavisnost izvlačenja znači nezavisnost od istorije."?

I gde sam napisao da li ima ili "To nema veze sa ravnomernošću ishoda (da su svi jednakoverovatni)."?

Verovatnoća/statistika je i primenjena na ovakvom slučaju. Primenio je vlasnik kazina (tj. lik koji je smislio rulet :)) u određivanju kvota na određene vrste klađenja. Na primer kvota da izađe broj 19 je 36 mada je šansa da izađe 1/37. Tu je u prednosti vlasnik kazina. Slično je i za crveno/crno i ostale igre na ruletu.

Ma kako da igraš posle velikog broja igara vlasnik je u plusu za neki mali procenat. To matematika garantuje vlasniku kazina.

Teško da ćeš da smisliš sistem da prevariš rulet :)

Pogledaj tekst na wikipediji i naćićeš koliko je kazino u prednosti.

To je tačno ali još uvek postoji mogućnost da mašina neuniformno raspodeljuje položaj kuglice. U tom slučaju postoji šansa da se nešto zaradi (bilo je takvih dogadjaja).

Ovde



Kakve veze imaju neuniformnost izbačenih brojeva i zavisnost izvlačenja od istorije o kojoj Miladin piše?

Ccc, tu ne stoji ni "Nezavisnost izvlačenja znači nezavisnost od istorije.",
niti stoji "To nema veze sa ravnomernošću ishoda (da su svi jednakoverovatni)."!

"neuniformnost izbačenih brojeva" može da se javi praktično kod svake mašine.

Mašina jednostavno zbog svoje nesavršenosti može da "forsira" neke brojeve ili boju. Koliko je to isplativo drugo je pitanje ali bilo je slučajeva da su ljudi uspeli da izvuku poveće sume. Pa je čak i bilo sudskih tužbi od strane kazina jer su igrači "provalili" mašinu.

Pokretač teme očigledno misli na zavisnost izvlačenja. Dakle, ovde se govori o neispravnosti mašine u tom pogledu.



Ovde se radi o neispravnosti mašine u pogledu neravnomernosti verovatnoća.

Zar "forsiranje" nekih brojeva ili boje ne povlači neravnomernost verovatnoća?

Na primer, udubljenje kod broja 0 "slučajno" je veće nego kod ostalih brojeva. Za očekivati je da će kuglica češće upadati u to udubljenje. Zato se broj 0 može pojaviti češće od 1/37. Na primer 2/37 puta. Tada se ostali brojevi javljaju 35/37 puta a kako je preostalih brojeva 36 tada će očigledno biti neravnomerna raspodela verovatnoća. Ili možda ima neka matematika kojom se i tada dobije uniformna raspodela? Znaš nešto o tome?

Da, to znači upravo to, ali postavljač teme pikira na zavisnost od istorije, što je nešto sasvim drugo.

Da li neko moze da prokomentarise Milanovu formulu:

n=log(31/37)/log(0.01)=26

Kad bi ona vazila u slucaju ruleta?