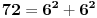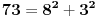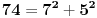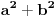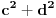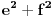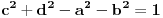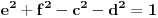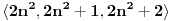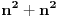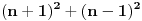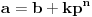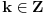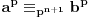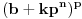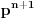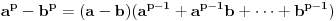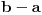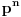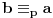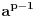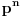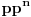[ Sini82 @ 01.07.2011. 17:10 ] @
|
[ Sherlock Holmes @ 01.07.2011. 17:51 ] @
Umes li da dokazes da postoji beskonacno mnogo Pitagorejskih trojki-tripleta? Imas Euklidov dokaz.
P.S. Da li je dovoljno dokazati da postoji beskonacno mnogo Pitagorejskih trojki? [Ovu poruku je menjao Sherlock Holmes dana 01.07.2011. u 19:05 GMT+1] [ Sini82 @ 01.07.2011. 18:14 ] @
Nije to ono što se u zadatku traži, treba dokazati da postoji beskonačno mnogo trojki uzastopnih prirodnih brojeva (svi oni ne mogu da budu potpuni kvadrati, razlika između dva potpuna kvadrata je uvijek veća od 1) koji se mogu napisati kao zbir dva potpuna kvadrata. Jedna takva trojka je 72, 73, 74.
[ Bojan Basic @ 01.07.2011. 18:32 ] @
[ Sini82 @ 01.07.2011. 20:27 ] @
Hvala ti Bojane, pomogao si mi. Napravio sam program koji traži slučajeve umjesto mene. Sumnjam da bi sam uspio da nađem pravilnost. Može li na neki drugi način da se dokaže tvrđenje zadatka ili mora da se "pogađa"?
Code: #include <math.h> #include <iostream> using namespace::std; bool provjera(int i) { int k=1; while (k*k<i) { if (sqrt(i-k*k)==(int)(sqrt(i-k*k))) { return true; } else if ((k+1)*(k+1)>i) return false; k++; } } void ispis(int i) { int k=1; while (k*k<i) { if (sqrt(i-k*k)==(int)(sqrt(i-k*k))) { cout<<i<<"="<<k<<"^2+"<<(int)(sqrt(i-k*k))<<"^2\n"; } else if ((k+1)*(k+1)>i) k=i; k++; } } main() { int* a; int n; cout<<"n="; cin>>n; int j; cout<<"\nTrazene trojke brojeva manjih od "<<n+1<<" su:\n"; for(j=1;j<=n-2;j++) { if (provjera(j)&&provjera(j+1)&&provjera(j+2)) { cout<<"\n("<<j<<", "<<j+1<<", "<<j+2<<")\n"; ispis(j); ispis(j+1); ispis(j+2); } } } Citat: n=1000 Trazene trojke brojeva manjih od 1001 su: (72, 73, 74) 72=6^2+6^2 73=3^2+8^2 73=8^2+3^2 74=5^2+7^2 74=7^2+5^2 (232, 233, 234) 232=6^2+14^2 232=14^2+6^2 233=8^2+13^2 233=13^2+8^2 234=3^2+15^2 234=15^2+3^2 (288, 289, 290) 288=12^2+12^2 289=8^2+15^2 289=15^2+8^2 290=1^2+17^2 290=11^2+13^2 290=13^2+11^2 290=17^2+1^2 (520, 521, 522) 520=6^2+22^2 520=14^2+18^2 520=18^2+14^2 520=22^2+6^2 521=11^2+20^2 521=20^2+11^2 522=9^2+21^2 522=21^2+9^2 (584, 585, 586) 584=10^2+22^2 584=22^2+10^2 585=3^2+24^2 585=12^2+21^2 585=21^2+12^2 585=24^2+3^2 586=15^2+19^2 586=19^2+15^2 (800, 801, 802) 800=4^2+28^2 800=20^2+20^2 800=28^2+4^2 801=15^2+24^2 801=24^2+15^2 802=19^2+21^2 802=21^2+19^2 (808, 809, 810) 808=18^2+22^2 808=22^2+18^2 809=5^2+28^2 809=28^2+5^2 810=9^2+27^2 810=27^2+9^2 Process returned 0 (0x0) execution time : 6.328 s Press any key to continue. [ Bojan Basic @ 03.07.2011. 00:39 ] @
Ovako kako si uradio — tražio od programa da ispiše sve trojke — dobio si mnogo „šuma“ i zato stvarno ne bi bilo lako naći pravilnost među tim rezultatima. Ja sam postupio malo drugačije: uočio sam da je u tvom primeru prvi član trojke zbir dva ista kvadrata, tj.
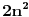 , pa sam potražio nekoliko takvih. Uz to se brzo uočava da je tada , pa sam potražio nekoliko takvih. Uz to se brzo uočava da je tada 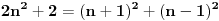 (bilo analizom pronađenih primera, bilo čak odmah), što svedoči da smo na dobrom putu — treba još samo uglaviti srednji član trojke. Opet ne treba puno vremena kako bi se ustanovilo da je u svim navedenim primerima srednji član trojke zbir oblika (bilo analizom pronađenih primera, bilo čak odmah), što svedoči da smo na dobrom putu — treba još samo uglaviti srednji član trojke. Opet ne treba puno vremena kako bi se ustanovilo da je u svim navedenim primerima srednji član trojke zbir oblika 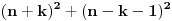 , za neko , za neko  . Onda postavimo jednačinu . Onda postavimo jednačinu 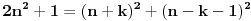 i dobijamo da ovo važi za i dobijamo da ovo važi za 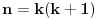 . .[ Sini82 @ 03.07.2011. 14:11 ] @
Dobro si uradio (upravo ono što se u zadatku traži, može da se nađe pravilnost postupajući na način koji si opisao), ja sam tražio opšti oblik za sve trojke (više nego što se u zadatku traži), zato nisam uspio. Još jednom hvala.
[ devetkamp @ 08.12.2012. 09:52 ] @
Jel moze neko da pomogne oko zadatka...
[ Sonec @ 08.12.2012. 13:18 ] @
[ Nedeljko @ 08.12.2012. 13:19 ] @
[ devetkamp @ 08.12.2012. 13:55 ] @
[ Sonec @ 08.12.2012. 14:13 ] @
Ja taj predmet ne mogu da nadjem medju predmetima na PMF-u u Nisu, na Matematici, nema veze.
A sta vi ucite iz te teorije brojeva? [ devetkamp @ 08.12.2012. 21:37 ] @
Stoji na sajtu.. medju prvim predmetima. Izmedju ostalog, radimo deljivost, sisteme ostataka, kongruencije, sisteme kongruencijskih jednacina... To je najtezi ispit, bar u prvom semestru... A radimo zadatke uglavnom sa olimpijada....
[ Sonec @ 08.12.2012. 22:14 ] @
Nasao sam, http://www.pmf.ni.ac.rs/pmf/predmeti/program/1504.pdf. Interesovalo me je samo sta se radi na drugim fakultetima iz predmeta Teorija brojeva i naisao sam na odgovor kakav sam i ocekivao (a koji je za mene razocaravajuci). Ne bih rekao da radite uglavno zadatke sa olimpijada, bar oni koje sam ja nasao http://www.pmf.ni.ac.rs/pmf/predmeti/1504/vezbe.php ne bi se mogli svesti pod tu kategoriju, al nema veze.
[ Nedeljko @ 08.12.2012. 22:25 ] @
A zašto bi se radili plimpijski zadaci, pa da niko ne može da pooži ispit? Meni se ovi zadaci sviđaju.
[ Sonec @ 08.12.2012. 22:33 ] @
Nisam rekao da mi je razocaravajuce sto se ne rade olimpijski zadaci, i ne bi trebalo da se rade. Samo me je interesovalo sta se podrazumeva pod predmetom Teorija brojeva i uvek cujem isto (kongruencije po modulu, itd.), a to me malo nervira (to sto se podrazumeva pod samim predmetom, ne mislim na kongruencije po modulu).
[ Nedeljko @ 08.12.2012. 23:32 ] @
A stvarno bode oči da nema ničega o raspodeli prostih brojeva.
[ Sonec @ 09.12.2012. 00:12 ] @
Ako si mislio na Prime number theorem onda je i logicno sto to ne rade, jer za njen dokaz je potrebno znanje iz Kompleksne analize (bar za dokaz koji ja znam), pa nije za ocekivati da se to drzi brucosima. Ali zato, sa druge strane, ocene Čebiševa ne zahtevaju neko preveliko znanje, zatim, asimptotske formule za odredjene funkcije i slicno, na primer. Sve zavisi (rekao bih) od predavaca i njegovog odabira kojom oblasti teorije brojeva ce njegov kurs stremiti (da li je to analiticka teorija brojeva, algebraska teorija brojeva ili nesto drugo). Al verujem da je bolje ovaj kurs ostaviti za starije godine, a da se ovakvi zadaci (koij su ovde bili razmatrani) rade u algebri, diskretnoj i slicnim predmetima.
[ Bojan Basic @ 09.12.2012. 00:42 ] @
Na novosadskom PMF-u u najnovijem (predstojećem) ciklusu akreditacije predmet Teorija brojeva nalazi se na trećoj godini jednog smera i na master studijama drugog smera. Pošto će meni biti poveren taj predmet (predavanja + vežbe), evo programa koji sam sastavio, možda će nekome biti zanimljiv.
Teorijska nastava: Uvodni pojmovi, mala Fermaova, Ojlerova i Vilsonova teorema. Red ostatka, primitivni koreni. Kvadratni ostaci. Zakon kvadratne recipročnosti. Klasični problemi o prostim brojevima. Diofantove jednačine. Pitagorejske trojke, istorijat velike Fermaove teoreme. Pelova jednačina. Reprezentacije brojeva sumama kvadrata. Proširenja prstena celih brojeva: Gausovi celi brojevi, prsten ℤ[√d]. Dalekosežne hipoteze teorije brojeva: Rimanova hipoteza, Šincelova hipoteza H, abc-hipoteza. Prikaz savremenih tokova teorije brojeva. Osnovni pojmovi o eliptičkim krivima. Osnovi analitičke teorije brojeva. (Poslednja dva naslova rade se samo na ovom smeru gde je predmet na master studijama.) Praktična nastava: Osnovna svojstva prostih brojeva i deljivosti. Primena kineske teoreme o ostacima. Primena male Fermaove, Ojlerove i Vilsonove teoreme. Rad sa kongruencijama višeg reda. Rešavanje i primena Pelove jednačine. Reprezentacije brojeva sumama kvadrata. Primena proširenja prstena celih brojeva. Kondicionalno rešavanje problema pod otvorenim pretpostavkama. [ Nedeljko @ 09.12.2012. 00:55 ] @
Sonec
Teorema se može učiti i bez dokaza, kao i njeno primenjianje. Bojane, zašto nisi ugurao teoremu o prostim brojevima, možda na račun nečega drugog? Da li će biti na sajtu nečega za nas neuke? [ devetkamp @ 09.12.2012. 08:50 ] @
Dobro, malo sam preterao, ali zaista ima i takvih zadataka... Zbirka koju koristimo je Uvod u teroiju brojeva ( Kadelburg, Micic, Djukic ), i tu zaista ima puno takmicarskih zadataka... Sto ume da bude tesko za nekog ko se prvi put srece sa tim gradivom... Uglavnom nam je problem, sto za svaki zadatak postoji nova ideja, nema "sablona" po kom se zadaci rade, i tesko da se bez prethodnog iskustva moze ostvariti dobar rezultat...
[ Bojan Basic @ 09.12.2012. 11:24 ] @
Citat: Nedeljko: Bojane, zašto nisi ugurao teoremu o prostim brojevima, možda na račŭn nečega drugog? Ako misliš na asimptotsku procenu, to je sadržano u delu „klasični problemi o prostim brojevima“. A u ovom delu „osnovi analitičke teorije brojeva“ planiram (možda preoptimistično, ali videćemo Citat: Nedeljko: Da li će biti na sajtu nečega za nas neuke? Zadataka sa kolokvijuma će biti sigurno (to imaš već i sada, pošto sam držao vežbe iz tog predmeta poslednjih godina). Što se teorije tiče, možda ću i neki oblik PDF-ova s predavanja kačiti na net, no o tom potom. Doduše, za kurs koji se sada drži (s nešto drugačijim programom od onog koji sam gore naveo) već imaš predavanja okačena na sajtu sadašnjeg predmetnog profesora, Igora Dolinke: http://sites.dmi.rs/personal/dolinkai/tb/l_notes.htm. [ Sonec @ 09.12.2012. 11:39 ] @
Evo Bojane, ako te interesuje, da kazem sta sam ja (do sada, posto mi je to predmet u ovom semestru) radio iz Teorije brojeva 1:
1. Aritmeticke funkcije i karakteri Abelovih grupa 2. Ocene Cebiseva za broj prostih brojeva 3. Generatorni Dirichletovi redovi aritmetickih funkcija 4. Dirichletova teorema o prostim brojevima u aritmetickim progresijama :) 5. Riemannova zeta-funkcija 6. Teorema o prostim brojevima 7. Integralna rasirenja prstena 8. Dedekindovi domeni To je to za sada, u planu je (koliko se stigne): 9. Prsteni celih brojnih polja 10. Grupa klasa ideala 11. Rascepljivanje i ramifikacija ideala pri rasirenjima prstena celih 12. Ocene Minkowskog 13. Dirichletova teorema o jedinicama u prstenima celih Preskoceno je (sto je profesor bio naumio, al je teska srca odustao): Selbergovo reseto i prosti brojevi blizanci [ Bojan Basic @ 09.12.2012. 12:03 ] @
Zanimljivo, hvala. Ovde skoro da i nema poklapanja s onim programom što sam ja pominjao, ali čini mi se da za to postoji relativno jednostavno objašnjenje. Naime, tvoj kurs očigledno je zamišljen kao kurs skoro isključivo analitičke teorije brojeva, dok ću ja analitičku teoriju brojeva raditi tek toliko da se stekne osećaj o njoj (i to samo na master studijama).
Ko to predaje u Beogradu, i ko drži vežbe? Sad da i ja postavim Nedeljkovo pitanje [ Sonec @ 09.12.2012. 12:27 ] @
Predavanja drzi profesor Goran Djankovic, jedan od mojih omiljenijih profesora (sto se ne bi moglo reci da je misljenje vecine studenata (s obzirom da je on do sada drzao vezbe iz Algebre 1 (bio je asistent do ove godine) i ljudi generalno nisu dobro prosli)). Fond casova je 2+2, s tim, da vezbe ne postoje (bilo je zamisljeno da profesor drzi i vezbe) vec su stalno predavanja (koja su odobrena od strane studenata (to da nemamo vezbe) s obzirom da drzi kurs "ozbiljnoj ekipi", nama sa Teorijske matematike na trecoj godini i tu nema slabih igraca :)).
Neke materijale mozes videti ovde http://poincare.matf.bg.ac.rs/~djankovic/predavanja4.htm, s tim, da tu i nema predavanja (osim Perronove formule) koja je on drzao nama ove godine, mozda ce kasnije biti nesto dodato iz algebarske teorije brojeva. Vise je okaceno kao dodatna literatura za zainteresovane. Tu imas okacene domace zadatke, ima ozbiljnih zadataka. Ne bih bas rekao da je kurs zamisljen kao skoro iskljucivo kurs iz analiticke teorije brojeva, pre bih rekao da je odnos analiticka/algebarska = 65/35 (s tendencijom da procenat algebre se poveca, u zavisnosti od toga koliko stignemo) :) Inace, da napomenem, kurs Teorija brojeva 1 se slusa i na L smeru (profesor matematike i racunarstva), njima drzi profesorka Dragana Todoric i tamo se radi uglavno algebarski deo (sto je bila praksa do sada na fakultetu, ovo sada je novina). Postoji nastavak kursa, na master studijama, zove se (zamislite) Teorija brojeva 2. [ Nedeljko @ 09.12.2012. 12:58 ] @
Mislim da mešaš algebarsku i klasičnu teoriju brojeva. Algebarska se bavi proučavanjem teorije brojeva putem algebarskih struktura povezanih sa njom, kao što se algebarska topologija bavi proučavanjem topoloških prostora putem algebarskih struktura koje imaju veze sa njima. Ako još nisi učio AT, onda je to nalik na proučavanje algebarskih jednačina preko teorije grupa.
[ atelago @ 13.12.2012. 10:44 ] @
Molim doktora Bašića da mi kaže koji matematičar je rekao da se svaki paran
broj može podeliti na dva prosta. Nešto sam pokušavao i došao do nekih rezultata. [ darkosos @ 13.12.2012. 11:25 ] @
[ Nedeljko @ 13.12.2012. 12:22 ] @
Naravno, to do sada nije dokazano, već ima status pretpostavke. Poverena je kompjuterski do neke vrednosti.
[ Sonec @ 13.12.2012. 14:06 ] @
Kad ste se vec dotakli toga, Terence Tao je relativno skoro dokazao http://arxiv.org/pdf/1201.6656v4.pdf
[ Nedeljko @ 13.12.2012. 17:03 ] @
Tamo je dokazano da je svaki neparan broj veći od 1 zbor najviše pet prostih brojeva, što je još uvek daleko od Goldbahove hipoteze.
[ Sonec @ 13.12.2012. 17:11 ] @
A gde sam rekao da je blizu?
[ Nedeljko @ 13.12.2012. 19:09 ] @
Nisi napisao ništa, pa se triče utisak kao da je dokazao Goldbahovu hipotezu.
[ Sonec @ 13.12.2012. 19:21 ] @
Svašta. Valjda je nekome jasna razlika izmedju brojeva 2 i 5 i pojma parnog i neparnog broja.
[ Bojan Basic @ 13.12.2012. 19:31 ] @
Ono što je Tao dokazao je pomak zapravo ka tzv. slaboj Goldbahovoj hipotezi, koja predviđa da se svaki neparan broj veći od 5 može zapisati kao zbir najviše tri prosta broja. Pre ovog rada najbolji rezultat bio je kao zbir najviše šest prostih brojeva, Tao je ovo spustio na pet.
No, slaba Goldbahova hipoteza znatno je lakša od Goldbahove hipoteze, budući da je za ovu prvu već poznato da važi do neke granice, kao i od neke granice (za „pravu“ Goldbahovu hipotezu rezultat ovog drugog tipa ne postoji, niti postoje ikakvi izgledi da bi se u skorije vreme tako nešto moglo dobiti), gde su obe granice poznati brojevi. Dakle, dovoljno je još popuniti rupu između njih. Pritom ta rupa čak uopšte nije strašna koliko bi mogla biti, jer provera da li je neki konkretan broj iz te rupe prost jeste u dosegu današnjih kompjutera. Zato verujem da će, uz još malo profinjavanja granica a takođe i rast kompjuterske moći, slaba Goldbahova hipoteza biti dokrajčena za najdalje nekoliko decenija (mnogi od nas svakako će to doživeti). Za „pravu“ Goldbahovu hipotezu pak je neophodan drastičan prodor na polju teorije, i to se može desiti sutra a može i tek za nekoliko vekova. [ Nedeljko @ 13.12.2012. 20:38 ] @
Ja mislim da će sutra.
[ Bojan Basic @ 13.12.2012. 20:48 ] @
@Nedeljko:
E, evo možemo taman sutra da se ponovo okupimo na ovoj temi pa vidimo jesi li u pravu. [ atelago @ 14.12.2012. 21:22 ] @
Ja sam kriv. Pa kad se okupimo ne bi trebalo da to dugo traje nego samo - malo sutra!
[ Bojan Basic @ 14.05.2013. 16:22 ] @
Citat: Bojan Basic: Zato verujem da će, uz još malo profinjavanja granica a takođe i rast kompjuterske moći, slaba Goldbahova hipoteza biti dokrajčena za najdalje nekoliko decenija (mnogi od nas svakako će to doživeti). Prilične su šanse da nećemo morati da čekamo čak ni ovoliko koliko sam prognozirao. Tehnika dokaza je, inače, upravo onakva kakvu sam prognozirao: korišćeni su dosadašnji metodi ali pronađen je način da se neke procene znatno poboljšaju, čime je slaba Goldbahova hipoteza dokazana za sve brojeve veće od 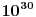 (prethodna granica iznosila je (prethodna granica iznosila je 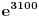 ). Ova granica ipak je nešto dalje od mesta dokle su kompjuterska proveravanja dobacila, no nađeno je i poboljšanje algoritma za proveru kompjuterom, doduše slabo ali taman dovoljno da se ova granica dohvati. ). Ova granica ipak je nešto dalje od mesta dokle su kompjuterska proveravanja dobacila, no nađeno je i poboljšanje algoritma za proveru kompjuterom, doduše slabo ali taman dovoljno da se ova granica dohvati.Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|