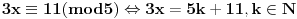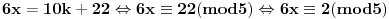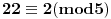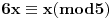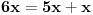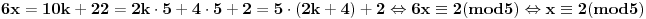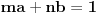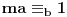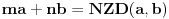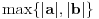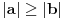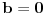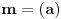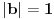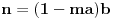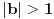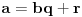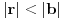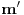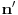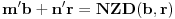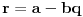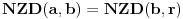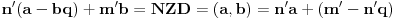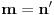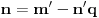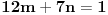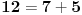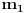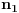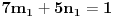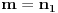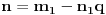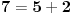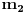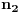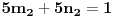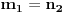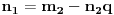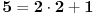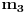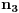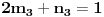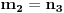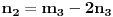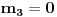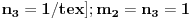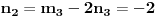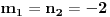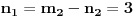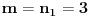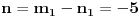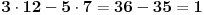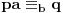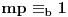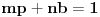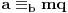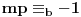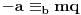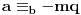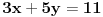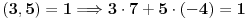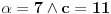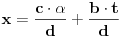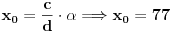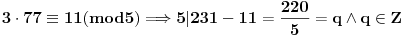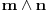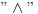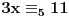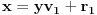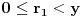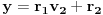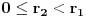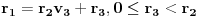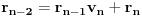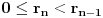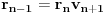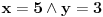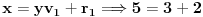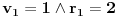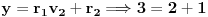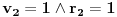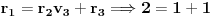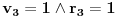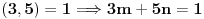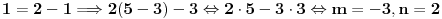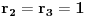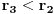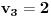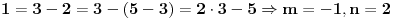ja mislim da je ovako, neveruj mi na rec, nek neko potvrdi da li je tacno :)


kada pomnozis sa 2 imas jer je i koristis da je , jer je
ili ovako

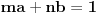
Celi brojevi i su uzajamno prosti akko postoje celi brojevi i takvi da je . U tom slučaju je .

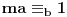
Kako naći brojeve i ? Opisaću takozvani prošireni Euklidov algoritam, kojim se pronalaze i takvi da je .

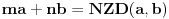
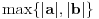
Kao meru složenosti ovog problema uzećemo veličinu . Pretpostavimo da je .

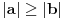
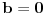
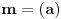
1. Ako je , onda je , dok se može izabrati proizvoljno.

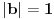
2. Ako je , onda se može izabrati proizvoljno, se određuje po formuli .

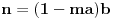
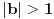
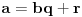
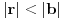
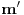
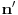
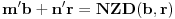
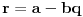
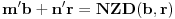
3. Ako je , onda najpre treba naći cele brojeve i takve da je i (tzv. delenjem sa ostatkom). Zatim naći cele brojeve i takve da je . Ovde treba primetiti da smo polazni problem sveli na problem iste vrste, ali manje složenosti, tako da se na njega primenjuje ista metoda sve dok se ne dođe do jednog od prethodna dva slučaja. Sada treba iskoristiti činjenicu da je i zameniti to u formuli . 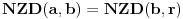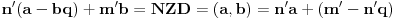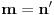Obzirom da je , zaključujemo da je , odakle sledi da treba uzeti i .

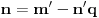
Primer:

Naći cele brojeve i takve da je .

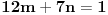
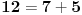
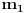
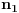
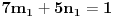
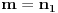
Obzirom da je nađimo i takve da je i stavimo i .

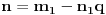
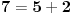
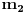
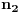
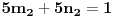
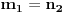
Obzirom da je nađimo i takve da je i stavimo i .

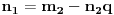
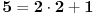
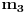
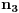
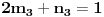
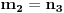
Obzirom da je nađimo i takve da je i stavimo i .

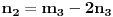
Recimo,

, , ;
, ;
, ;

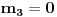
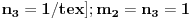
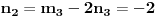
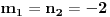
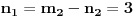
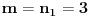
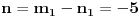
Provera: .

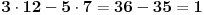
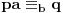
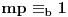
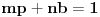
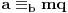
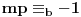
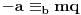
E sad, kad imaš kongruenciju sa poznatim i i uzajamno prostim i , onda najpre treba da nađeš takvo da je , to jest i takve da je . Zapravo, tebi treba samo , koga u slučaju malih vrednosti možeš naći običnim pogađanjem. Tada je . Profesorka očigledno ponekad koristi vrednosti za koje je , kada je , odnosno .

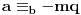
Sad rijesi ,,



Provera:

@Nedeljko
Mogu li se brojevi naci prostim Euklidovim algoritmo,mislim ja znam da nadjem jednim Euklidovim algoritmo brojeve al to nije ovaj koji si ti koristio.

Prvo, znak nije prosta zamena za veznik "i" u Srpskom jeziku, već iskazni logički veznik, koji dakle povezuje iskaze u složeniji iskaz koji je tačan akko su oba sastavka tačna.

Drugo, nisi opisao algoritam koji koristiš, pa ti ne mogu odgovoriti na pitanje.

Evo kako bih nasao u zadatku
To bi bio ovaj algoritam:
,
,

,

.
Imam sad da je
,za
,za
,za
Iz cega zakljucejemo da je
Dalje dobijam:
I tako bi dobio te brojeve i .

Koliko vidim, kod tebe je , što nije u skladu sa . Rekao bih da si ovo hteo da kažeš:


,za
,za
,za

.

Ako je to to, onda bih rekao da se radi o istom algoritmu.

Da,to sam htio da odradim nego zeznuo sam se u racunu nisam vodio racuna o postvavlejnom uslovu.
I nisam primetio da se radi o istom algoritmu.