Ti uvek možeš da naštimaš cele brojeve

i

tako da bude
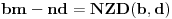
. Otuda mora da
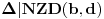
. Slično važi i
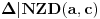
. Dakle, postoje celi brojevi
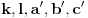
i
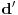
takvi da je
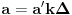
,
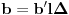
,
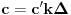
i
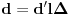
, odakle je
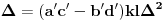
,
odakle
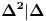
, pa je
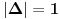
. Jasno je da je taj uslov i dovoljan.
E, sad, to je slučaj kada je determinanta sistema različita od nule. Ostalo je da dokažeš da se u slučaju da je determinanta sistema jednaka nuli uvek mogu izabrati celi brojevi

i

tako da sistem nema nijednog rešenja, pa ni celobrojnog.