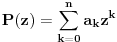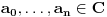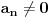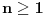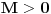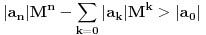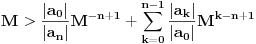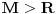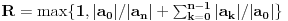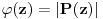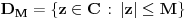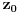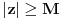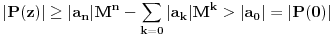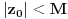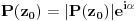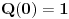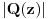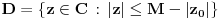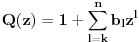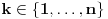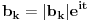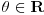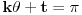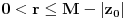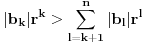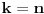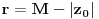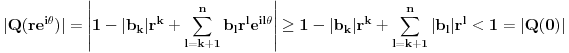[ Sonec @ 03.07.2011. 17:35 ] @
Stav. Ako je polinom 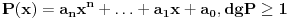 (nekonstantan), (nekonstantan), 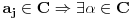 tako da je tako da je 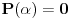 . (dg - stepen) . (dg - stepen)Interesuje me dokaz ovog stava, al koji sadrzi sledece elemente (tj. kako je nama profesor dokazao, a niko nije razumeo): -prvo se koristi uopstenje Vajerstrasove teoreme nad kompleksnim brojevima (sta god to bilo (znam sta je Vajerstrasov stav (za neprekidnu f-ju)) -zatim se koristi trigonometrijski oblik kompleksnog broja -i zatim sledi dokaz samo stava, koji je poprilicno konfuzam (i sam se profesor zapetljao, pa je "standardno" smutio dokaz): 1.standardno, polazi se od PPS (pretpostavimo suprotno), konstruise se odredjena f-ja  , dokazuje se da ona ima minimum , dokazuje se da ona ima minimum2.bez gubitka na opstosti 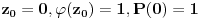 , , 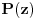 zamenimo sa zamenimo sa 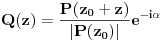 ..... .....3.  ..... .....Ako neko zna gde moze da se nadje ovakav dokaz (al iskljucivo ovakav) bio bih mu zahvalan da mi kaze. P.S ovaj dokaz http://en.wikipedia.org/wiki/Fundamental_theorem_of_algebra nije to sto mene interesuje |