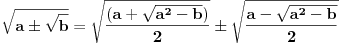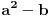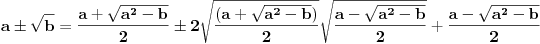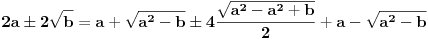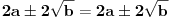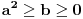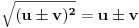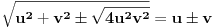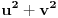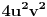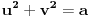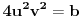Pa ovako (naravno, nisi napomenuo, ali mora biti ispunjeno da je puni kvadrat!):
(Prvo se kvadrira identitet).
Dobija se:

Zatim se zadnja jednacina pomnozi sa 2:

Posle ponistavanja suprotnih izraza, dobija se identitet

Znaci, dokaz je zavrsen!

Ne mora, već samo treba da bude .

To je bio dokaz, on je trazio izvodjenje!

Da,i kad sam postavljo temu mislio sam da ce mi se neko javiti sa dokazom,i htio sam da napisem da dokaz znam da uradim nego mi treba izvodjenje ali opet reko skontace valjda,da nisam trazio dokaz nego izvodjenje.

Znaci znam dokazivanje da radim,ali mi je potrebno izvodjenje.

<sub>[Ovu poruku je menjao edisnp dana 07.07.2011. u 21:01 GMT+1]

[Ovu poruku je menjao edisnp dana 07.07.2011. u 21:02 GMT+1]</sub>

E onda izvinite, igra reci, uopste nisam primetila... Nekako po automatizmu! Slobodno obrisite!

Nemora da se brise koristice ce nekom sigurno,jos da tema upotpuni sa izvodjenjem i bilo bi super.

?

(1)

Pojednostavimo izraz na lijevoj strani, zamijenimo sa , sa .



____________

Rješavanjem sistema po i i uvrštavanjem u (1) dobijamo Langranžov identitet.

Može li neko da mi objasni ovo?

A ako moze i meni jedno objasnjenje u vezi ovog

_{[Ovu poruku je menjao SrdjanR271 dana 07.07.2011. u 19:37 GMT+1]}

ahahahahahahahahahahahahahahahahahahahahaha

Pardon ,Pardon ,Pardon evo i ja se sad smejem koliko mogu verujte al nemora pravit neku komediju od toga,hahahahahahha,hahahahha.Bas mi je neprijatno.
I usput da se zahvalim Sini82 na odgovoru hvala.

Ozbiljno, šta podrazumevate pod dokazom, a šta pod izvođenjem?

Izvodjenje je kako je neko prvi put dosao od jednacine sa leve strane do one na desnoj, dok je dokaz kako da dokazes da to na desnoj jeste jednako onome na levoj.

Bar ja mislim da je to u pitanju.

Jednakost je relacija ekvivalencije.
Jedna od osobina relacije ekvivalencije je simetričnost.
L=D sledi D=L.

Kako mi da pogodimo "kako je neko prvi put prešao sa leva na desno"?
Peške sigurno.
Sigurno nije onako elegantno kao Sini82.
Lagranž je probavao, probavao,.... i pogodio.

Izuzimajući dokaz indukcijom, ne vidim razliku između izvođenja i dokaza.
Gaus je izveo: 1+2+3+4+...n = n*(n+1)/2 a može se i dokazati indukcijom.


Pitagorinu teoremu ne znam izvesti (prevesti levo na desno) ali znam dokazati.

Da mogu sam da dobijem neku formulu ,bez toga da moram da je pamtim ,a sto se tice dokaza,da dokazem ono sto sam dobijo ili ti sto sam izveo na primer,da je tacno.

@Sini82 ti je vec dao princip, ali pogledaj i ovo http://planetmath.org/encyclop...ngSquareRootAlgebraically.html i http://www.physicsforums.com/showthread.php?t=303777 u pitanju su kompleksni brojevi ali princip je isti

Pretpostavljam da oni koji žele izvođenje, žele dokaz jednakosti transformisanjem samo leve, tj. bez transformisanja desne strane jednakosti.

Način da se to uradi očigledan je već iz Janinkinog dokaza :


<sub>[Ovu poruku je menjao berazorica dana 08.07.2011. u 11:57 GMT+1]


[Ovu poruku je menjao berazorica dana 08.07.2011. u 12:01 GMT+1]</sub>

Ja mislim da je pitanje:"Moze li neko da mi pokaze kako se izvodi Langrazev Identitet:

Odatle je krenulo naklapanje:Kakva je razlika između izvođenja neke formule i dokazivanja valjanosti neke formule?

Nije čovjek pitao da li je formula dobra nego kako je neko do nje došao.

1)Da li je intuitivno lupio pa onda dokazao da vrijedi,dakle intuicijom.
2)Deduktivno,postepeno nekim metodama došao od poznatih znanja do one formule.

Čovjek je pretpostavio da je to 2) i onda lijepo pita ;kako?
A onda mu vi kažete da je svejedno da li je to bilo metodom 1) ili 2).

To je bezvezni odgovor,ali nažalost tačan.Kao da ste mu odgovorili da se cipele prave od kože što je takođe nažalost tačno,ali to čovjeka ne zanima.

<sub>Bojan Bašić: uklonjeni delovi koji su se odnosili na obrisane poruke.

[Ovu poruku je menjao Bojan Basic dana 12.07.2011. u 14:24 GMT+1]</sub>

U jednom trenutku se stiglo do pitanja o razlici između izvođenja i dokazivanja, a kandorus je naveo kao primer izvođenje obrasca za brzinu preko izvoda. Onda je upitan za definiciju brzine napisao onaj integral.



Meni je tek sad jasno koja je razlika između dokazivanja i izvođenja. Dokazivanje formule podrazumeva da već imamo formulu, a izvođenje je postupak dolaženja do formule. OK, to ima smisla. Neki su već dali odgovore u tom pravcu, ali do sada nisam shvatao o čemu se radi.

<sub>Bojan Bašić: uklonjeni delovi koji su se odnosili na obrisane poruke.

[Ovu poruku je menjao Bojan Basic dana 12.07.2011. u 14:24 GMT+1]</sub>

Da odgovorim na početno pitanje teme.

Od izraza sa desne strane lako je doći do izraza na levoj strani kvadriranjem, pa korenovanjem. Međutim, ako treba od leve strane dobiti desnu, prvo što se vidi je da je izraz na desnoj strani daleko složeniji, pa je pravo pitanje zašto bi neko komplikovao izraz. Lagranžu je takav oblik trebao za nešto. Treba prvo videti šta mu je trebalo, pa onda dešifrovati kako je izveo to što mu je trebalo.

Mene interesuje Nedeljko, koja je razlika izmedju izvodjenja i dokaza? Ostao sam uskracen za taj odgovor.
P.S. Da li je uopste ima?

Pa, nisi ostao uskraćen. Evo:



<sub>Bojan Bašić: uklonjeni delovi koji su se odnosili na obrisane poruke.

[Ovu poruku je menjao Bojan Basic dana 12.07.2011. u 14:25 GMT+1]</sub>