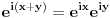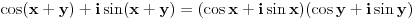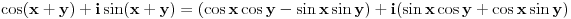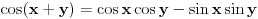[ edisnp @ 11.07.2011. 14:04 ] @
|
[ SrdjanR271 @ 11.07.2011. 17:06 ] @
Citat: edisnp: Da li bi mogao neko da mi pokaze ili da dobijem neko upustvo kako da preko formule: 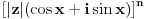 ,izvedem neki trigonometrijski identitet. ,izvedem neki trigonometrijski identitet.Pre svega ovo je Moavrova formula: 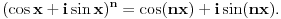 Može da se dokaže indukcijom, ili preko Ojlerove formule. Ovo je Ojlerova: 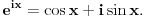 Nekad je pišu kao cis(x). Nekad je pišu kao cis(x).A ovo, 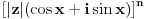 , je stepen kompleksnog broja u trigonometrijskom obliku. , je stepen kompleksnog broja u trigonometrijskom obliku.[ edisnp @ 11.07.2011. 17:35 ] @
Hvala puno na pomoci!
[ edisnp @ 11.07.2011. 17:45 ] @
@Srdjan Imas li vrijemena da da je dokazes Preko Ojlerove formule.?
[ SrdjanR271 @ 11.07.2011. 17:53 ] @
Idem da kupim nešto. Za pola sata, cu dokazati Ojlerovu, a iz nje Moavrovu.
[ igorpet @ 11.07.2011. 18:55 ] @
Evo npr. dokaza Ojlerove preko redova ... http://resonanceswavesandfield...ation-and-complex-numbers.html ili npr. ovako https://ccrma.stanford.edu/~jos/mdft/e_j_theta.html a dokaz Moavrove moze npr. i ovako https://ccrma.stanford.edu/~jo.../Direct_Proof_De_Moivre_s.html
Baci pogled i na prikaceni .pdf ima interesantnih zanimljivosti a spominje se i Ojlerova jednacina - cisto informativno [Ovu poruku je menjao igorpet dana 11.07.2011. u 20:13 GMT+1] [ SrdjanR271 @ 11.07.2011. 19:44 ] @
Dokaz Ojlerove formule preko redova.
Proširene definicije za exp(x), sin(x) i cos(x) iz realne analize su: 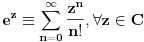 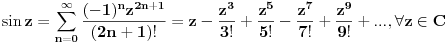 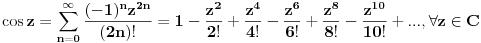 Ako sada uzmemo da je 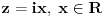 , imamo sledeće: , imamo sledeće: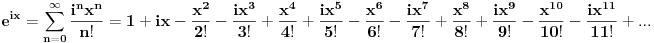 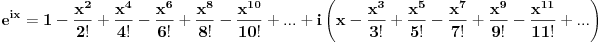 (1) 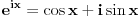 Formula (1) je poznata kao Ojlerova formula. (*) 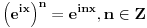 Pa na osnovu formule (1) i osobine (*) imamo : 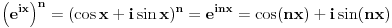 odnosno (2) 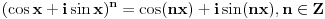 Formula (2) je poznata kao Moavrova formula. [Ovu poruku je menjao SrdjanR271 dana 11.07.2011. u 20:58 GMT+1] [ petarm @ 11.07.2011. 19:51 ] @
@ igorpet
Prikaceni pdf je deo iz knjige "Matematicki vremeplov". Ja sam kupio tu knjigu na Spensu u Novom Sadu. Kostala je oko 400 dinara. [ SrdjanR271 @ 11.07.2011. 20:04 ] @
Citat: edisnp: Da li bi mogao neko da mi pokaze ili da dobijem neko upustvo kako da preko formule: 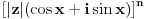 ,izvedem neki trigonometrijski identitet. ,izvedem neki trigonometrijski identitet.Pogledaj ovo http://demonstrations.wolfram....ivresTheoremForTrigIdentities/. [ Nedeljko @ 11.07.2011. 21:12 ] @
Ima u toj knjizi grešaka. Recimo, Muavr je dokazao da postoji konstanta
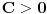 takva da je takva da je 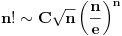 , izrazio tu konstantu preko beskonačnog reda, dok je Stirlingova zasluga što je dokazao da je ta konstanta jednaka , izrazio tu konstantu preko beskonačnog reda, dok je Stirlingova zasluga što je dokazao da je ta konstanta jednaka 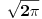 . .Za Tejlorovu formulu mislim da je znao još Njutn, ali je to utvrđeno tek nakon njegove smrti pregledom njegovih neobjavljenih radova. [Ovu poruku je menjao Nedeljko dana 11.07.2011. u 23:29 GMT+1] [ igorpet @ 11.07.2011. 21:32 ] @
Citat: petarm: @ igorpet Prikaceni pdf je deo iz knjige "Matematicki vremeplov". Ja sam kupio tu knjigu na Spensu u Novom Sadu. Kostala je oko 400 dinara. Nemam konkretno tu knjigu, ali ima dosta literature na engleskom koje se bave ovim temama a postoji i vise knjiga na srpskom i one su otprilike kompilacije vec poznatih stvari i zanimljivosti koje su vekovima ostale takve kakve ih mi danas znamo, i ako cinjenice govore da bi mozda pravednije bilo da su drugacije, mada to sada nije toliko ni bitno. Ljudi su vekovima proucavali tudje radove, dopunjavali ih, usavrsavali i pomalo kraduckali i eto usli u istoriju najverovatnije sasvim opravdano ali postoje slucajevi da se nikad nisu ogradili da to nije bas njihova "originalna" ideja ... toga je uvek bilo i bice. A pojedini zaključci do kojih su oni dosli pre vise vekova ili milenijuma i danas predstavljaju enigmu za vecinu ljudi, pa cak i za one koji su odabrali matematiku kao zanimanje, i to je ono sto je u stvari genijalno u njihovim zaključcima - prevazišli su svoje vreme definitivno ali dobrim delom i naše ... a bez toga današnji tehnološki napredak ni izbliza ne bi bio ovakav ... Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|