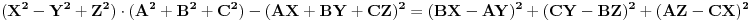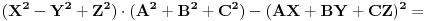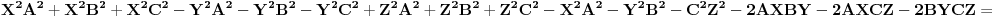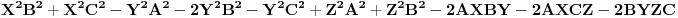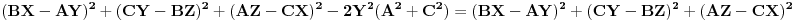[ Sherlock Holmes @ 11.07.2011. 17:37 ] @
|
[ Nedeljko @ 11.07.2011. 19:43 ] @
Razmotaš levu stranu jednačine, kao što si već uradio. Zatim razmotaš isto tako i desnu stran u jednakosti i onda uporediš to dvoje.
[ edisnp @ 11.07.2011. 19:56 ] @
A i mogo bi lijevu stranu jednacine da rastavis na cinioce da dobijes iste binome kao i na desnoj strani.
[ igorpet @ 11.07.2011. 22:57 ] @
Ja sam stigo do ovde:
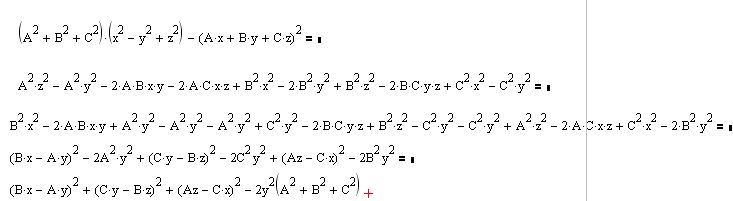 Siguran si da u zadatku ne postoji još neki uslov? U ovom identitetu leva i desna strana nisu jednake. [ edisnp @ 11.07.2011. 23:06 ] @
[ igorpet @ 11.07.2011. 23:06 ] @
Osim ako nisu mislili:
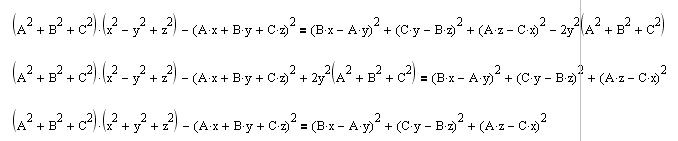 [ SrdjanR271 @ 11.07.2011. 23:33 ] @
[ Sherlock Holmes @ 12.07.2011. 07:49 ] @
Nema nikakvih drugih uslova. Samo pise dokazi Lagranzeve identitete. Ima jos par Diofantovih, ali su laki. I ja sam pokusavao dosta puta da uradim... Izbacio sam zadatak, jer sam mislio da sam napravio neki vrlo glupu gresku, a nisam je primetio. Al' izgleda da je 100% greska u postavci. Zadatak je iz Zbirka resenih zadataka iz algebre - Vene Bogoslavov. Nema nista u resenju, jer kod zadataka- Dokazi, vrlo retka pisu resenja, osim ako je komplikovaniji dokaz. Hvala svima!
[ Kolins Balaban @ 12.07.2011. 11:14 ] @
Vene-ove zbirke su prepune gresaka, kako u postavkama zadataka, tako i u rjesenjima. Nemoj se mnogo oslanjati na ono sto u njima pise.
[ fLuXx @ 12.07.2011. 12:41 ] @
 Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|