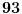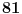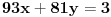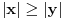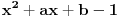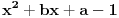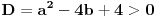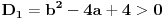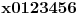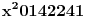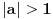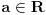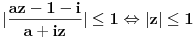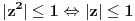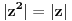[ Nuh @ 12.07.2011. 13:38 ] @
|
[ miki069 @ 12.07.2011. 14:44 ] @
1. Zadatak
Euklidov algoritam: 93 = 1*81 + 12 81= 6*12 + 9 12 = 9*1 + 3 3 = 12-9*1 = 12 - (81-6*12) = 7*12-81 = 7*(93-81) -81 3=7*93-8*81 Ne razumem o kom uslovu pričaš? 2. Zadatak nije da nađeš koja ima realne nule, već da bar jedna od njih 2 ima realne nule. Pretpostavi da su obe diskriminante negativne i dokaži protivurečnost. 3. Ne razumeju ni oni koji su radili. Napiši u Latex-u ili okači sliku. 4. Jel znaš šta je moduo kompleksnog broja? Jel znaš kako se dele 2 kompleksna broja? [ Sherlock Holmes @ 12.07.2011. 15:52 ] @
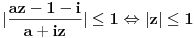 je isto sto i je isto sto i 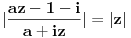 . Zar ne? Tebi se trazi da dokazes ovaj identitet, ali moras znati deljenje kompleksnih brojeva, sta je . Zar ne? Tebi se trazi da dokazes ovaj identitet, ali moras znati deljenje kompleksnih brojeva, sta je 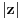 i cemu je jednako, tj. kako se moze napisati preko realnog i imaginarnog dela kompleksnog broja. i cemu je jednako, tj. kako se moze napisati preko realnog i imaginarnog dela kompleksnog broja. Kod drugog zadatka, ja sam imao ideju da se resi po 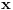 ova jednacina, i da se postavi uslov da je jedno resenje u intervalu ova jednacina, i da se postavi uslov da je jedno resenje u intervalu 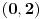 , i dobije se sistem nejednacina, a za drugo resenje napisemo da je u intervalu , i dobije se sistem nejednacina, a za drugo resenje napisemo da je u intervalu 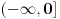 i i 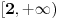 , tj. da je , tj. da je 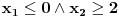 E,sad nisam siguran da moze ovako. E,sad nisam siguran da moze ovako.[ Nedeljko @ 12.07.2011. 16:26 ] @
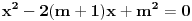 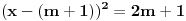 Da bi imala realna rešenja, mora da bude 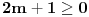 , odnosno , odnosno 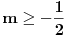 . .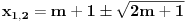 . .Imamo dva slučaja: a) 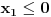 i i 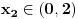 . .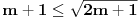 , , 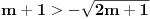 , , 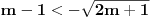 . .Obzirom da je 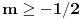 , prvi ulslov je ekvivalentan uslovu , prvi ulslov je ekvivalentan uslovu 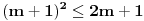 , a koji je ekvivalentan sa , a koji je ekvivalentan sa 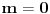 , dok je drugi uslov automatski ispunjen. Što se trećeg uslova tiče, obzirom na prvi uslov, dovoljno ga je proveriti za , dok je drugi uslov automatski ispunjen. Što se trećeg uslova tiče, obzirom na prvi uslov, dovoljno ga je proveriti za 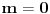 , kada nije ispunjen. , kada nije ispunjen.b) 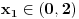 i i 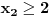 . .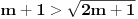 , , 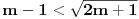 , , 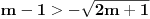 . .Obzirom da je 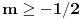 , prvi ulslov je ekvivalentan uslovu , prvi ulslov je ekvivalentan uslovu 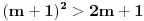 , a koji je ekvivalentan sa , a koji je ekvivalentan sa 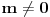 , dok je drugi uslov automatski ispunjen za , dok je drugi uslov automatski ispunjen za  , dok je u slučaju da je , dok je u slučaju da je 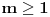 ekvivalentan uslovu ekvivalentan uslovu  . Treći uslov je ekvivalentan uslovu . Treći uslov je ekvivalentan uslovu 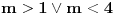 , tj. zadovoljen je za svako , tj. zadovoljen je za svako 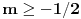 . .Dakle, 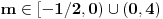 . .[ Nedeljko @ 12.07.2011. 16:30 ] @
[ Sherlock Holmes @ 12.07.2011. 16:39 ] @
Dobro, jasno mi je kod kompleksnih brojeva. Samo mi nije jasno kod ove jednacine, tacnije kod postavljanja uslova. Dakle, ti si podelio na dva slucaja. Kod prvog slucaja si napisao da je
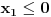 i i 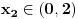 , zar ovde ne treba da se doda uslov da je , zar ovde ne treba da se doda uslov da je 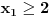 ? Isto tako kod drugog slucaja, zar ne treba da se doda uslov da je ? Isto tako kod drugog slucaja, zar ne treba da se doda uslov da je 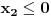 ? To mi nije jasno, ako mozes, objasni mi. ? To mi nije jasno, ako mozes, objasni mi.[ Nuh @ 12.07.2011. 17:39 ] @
Sto se tice prvog zadatka moze li neko da mi opet pokaze na jos jednom primeru da odradim isti je zadatak vama nista ne znaci a meni puno sad je ovaj primer,
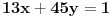 , ,A drugi zadatak sam poceo kao sto mi je Miki rekao al opet nedobijam nista ne znam kako. Sto se tice treceg zadatka nisam bio primetio da na resenjima ima postavljen rezultat ,evo na resenju pise 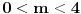 ,i sto se toga tice totalno sam zbunjen,. ,i sto se toga tice totalno sam zbunjen,.[ Nedeljko @ 12.07.2011. 18:38 ] @
Citat: Sherlock Holmes: Dobro, jasno mi je kod kompleksnih brojeva. Samo mi nije jasno kod ove jednacine, tacnije kod postavljanja uslova. Dakle, ti si podelio na dva slucaja. Kod prvog slucaja si napisao da je 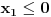 i i 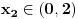 , zar ovde ne treba da se doda uslov da je , zar ovde ne treba da se doda uslov da je 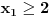 ? Isto tako kod drugog slucaja, zar ne treba da se doda uslov da je ? Isto tako kod drugog slucaja, zar ne treba da se doda uslov da je 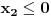 ? To mi nije jasno, ako mozes, objasni mi. ? To mi nije jasno, ako mozes, objasni mi.Pa, ne može da bude istovremeno 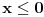 i i 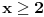 , već najviše jedno od to dvoje. , već najviše jedno od to dvoje.[ miki069 @ 12.07.2011. 18:57 ] @
45= 3*13 + 6
13= 2*6 + 1 1 = 13 - 2*6 = 13 - 2*(45 - 3*13) = 7*13 - 2* 45 7*13 - 2*45 = 1 X=7, Y=-2 Jel znaš Euklidov algoritam za nalaženje NZD-a ? Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|