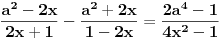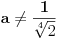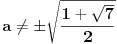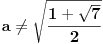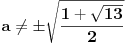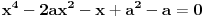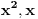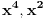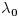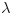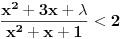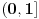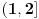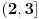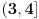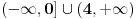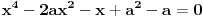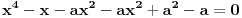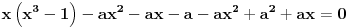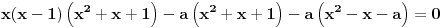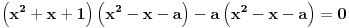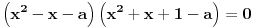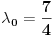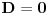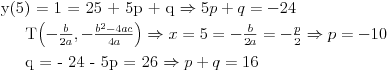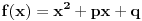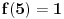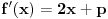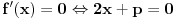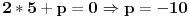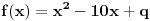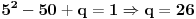[ Sherlock Holmes @ 14.07.2011. 02:38 ] @
|
[ SrdjanR271 @ 14.07.2011. 03:33 ] @
Citat: Sherlock Holmes: Sredjivao sam ovu jednacinu, prebacio sam sve na levu stranu i dobijem jednacinu 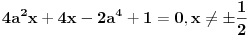 Ne znam kako dalje. Ja sam mislio cu kada sredim ovu jednacinu dobiti kvadratnu jednacinu po Ne znam kako dalje. Ja sam mislio cu kada sredim ovu jednacinu dobiti kvadratnu jednacinu po 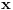 , pa da postavim uslov da je , pa da postavim uslov da je 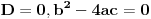 Onda bih dobio kvadratnu jednacinu ili bikvadratnu po Onda bih dobio kvadratnu jednacinu ili bikvadratnu po 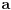 , to resim i dobijem vrednost realnog parametra , to resim i dobijem vrednost realnog parametra 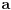 Ali se sve iskomplikovalo. Moguce je i da sam negde u racunu pri sredjivanju jednacine pogresio. Ali se sve iskomplikovalo. Moguce je i da sam negde u racunu pri sredjivanju jednacine pogresio.Rešiš po x, i dobiješ 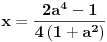 . .Sad samo vidiš kad je 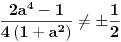 . .Ispostaviće se da je to ispunjeno pod C). Toliko od mene, odoh da spavam. [ Sherlock Holmes @ 14.07.2011. 09:57 ] @
Hvala puno! Prva dva su mu jasna. Ali kod treceg, ako mozes samo malo da mi pojasnis. Imam pocetnu jednacinu
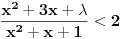 , kada prebacim , kada prebacim 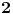 na levu stranu dobijem nejednacinu na levu stranu dobijem nejednacinu 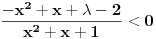 Posto je polinom Posto je polinom 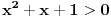 za svako realno za svako realno 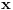 , tada postavljam uslov da je , tada postavljam uslov da je 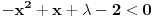 Ova nejednakost ce biti ispunjena za svako realno Ova nejednakost ce biti ispunjena za svako realno 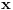 ako je ako je  . Postavim tu nejednakost i dobijem da je . Postavim tu nejednakost i dobijem da je 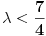 Do ovoga sam uspeo da dodjem kada sam resavao zadatak, ali ne znam sta dalje... Je l' moze malo objasnjenje? A, Do ovoga sam uspeo da dodjem kada sam resavao zadatak, ali ne znam sta dalje... Je l' moze malo objasnjenje? A, 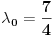 je tacno resenje, pripada intervalu je tacno resenje, pripada intervalu 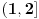 , sto je i resenje zadatka. , sto je i resenje zadatka. [ Nedeljko @ 14.07.2011. 10:28 ] @
Rečeno je da je za tu vrednost parametra jednakost tačna za sve realne vrednosti promenljive, osim za jednu. Ovo što si ti izračunao je skup vrednosti parametra za koje je nejednakost tačna za sve vrednosti parametra, a to nije ono što se traži. Pročitaj bolje zadatak.
[ Sherlock Holmes @ 14.07.2011. 10:36 ] @
[ Nedeljko @ 14.07.2011. 14:29 ] @
Da.
[ Sherlock Holmes @ 14.07.2011. 20:08 ] @
Najmanja vrednost izraza
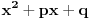 je je 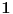 i dostiže se za i dostiže se za 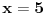 . Vrednost zbira . Vrednost zbira 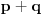 je: je:A) 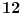 ; B) ; B) 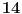 ; C) ; C) 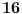 ; D) ; D) 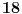 ; E) ; E) 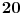 Pokušavao sam da uradim ovaj zadatak tako što sam postavio vrednost izraza da je 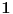 i da je i da je 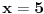 . Dobijem jednačinu . Dobijem jednačinu 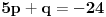 . Pošto imaju dve nepoznate, pokušao sam da dobijem sistem od dve jednačine sa dve nepoznate. Znamo za formulu za teme funkcije, koje se obeležava . Pošto imaju dve nepoznate, pokušao sam da dobijem sistem od dve jednačine sa dve nepoznate. Znamo za formulu za teme funkcije, koje se obeležava 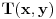 . Ovde je . Ovde je 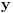 najmanja vrednost izraza, najmanja vrednost izraza, 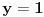 . Formula za izračunavanje . Formula za izračunavanje 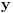 preko koeficijenata kvadratne jednacine je preko koeficijenata kvadratne jednacine je 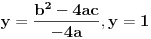 . Dobijem jednacinu . Dobijem jednacinu 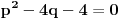 . I, sad imam sistem od dve jednačine sa dve nepoznate. Ali, sad nastaje problem. Izrazim . I, sad imam sistem od dve jednačine sa dve nepoznate. Ali, sad nastaje problem. Izrazim 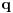 iz iz 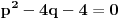 i dobijem da je i dobijem da je 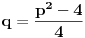 . Kada . Kada 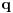 ubacim u prvu jednacinu, ubacim u prvu jednacinu, 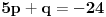 , dobijem kvadratnu jednacinu , dobijem kvadratnu jednacinu 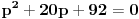 . Kada je rešim po . Kada je rešim po 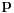 dobijem da je dobijem da je 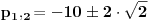 . I sad ne znam sta da radim, imam dve vrednosti za . I sad ne znam sta da radim, imam dve vrednosti za 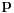 , kada to zamenim u drugu jednacinu da dobijem , kada to zamenim u drugu jednacinu da dobijem 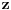 , dobicu takođe 2 rešenja , dobicu takođe 2 rešenja 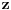 . Je l' moglo drugačije da se radi, da se izbegnu ova dupla rešenja? . Je l' moglo drugačije da se radi, da se izbegnu ova dupla rešenja? [ Sherlock Holmes @ 14.07.2011. 21:17 ] @
Uuh, da, da... Samo sam zakomplikovao. Zadaci su sa pripremnog matemarijala za prijemni iz matematike na MATF. Radim to po malo, pa nadje se po neki zadatak koji ne uspem da uradim. Hvala puno!
[ igorpet @ 14.07.2011. 21:35 ] @
Citat: Sherlock Holmes: ... Zadaci su sa pripremnog matemarijala za prijemni iz matematike na MATF... Da li imas specijalizovanu zbirku koja sadrzi zadatke u skladu sa programom polaganja prijemnog ispita? Da li znas gde moze da se nadje ova zirka u elektronskom obliku? [ Sherlock Holmes @ 14.07.2011. 21:41 ] @
Imam je u pdf formatu. I moze da se nadje na internetu, samo ne znam da li smeju da se ostavljaju linkovi, nelegalno skidanje. Mogu ti poslati preko PP ako ovde nije dozvoljeno. Imas PP od mene, pogledaj.
[ SrdjanR271 @ 15.07.2011. 09:23 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|