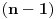[ Farenhajt @ 26.07.2011. 06:13 ] @
| Ako je dat trougao ABC, njegove stranice možemo obeležiti kao AB ili BA, AC ili CA, BC ili CB. Želimo sve njegove stranice da stavimo na spisak (tačno po jedanput), ali tako da, za svake dve susedne stavke na spisku, krajnja tačka prethodne stavke bude različita od početne tačke naredne stavke. Ilustracija: Spisak AB-BC-AC nije dozvoljen jer se "B" u AB podudara sa "B" u BC. Isto važi i za BA-BC-CA. S druge strane, svi naredni spiskovi su dozvoljeni: AB-AC-BC, BC-AB-CA, CA-CB-AB itd. Primedba: Spiskovi su linearni, a ne kružni, te stoga odnos između početne tačke prve stavke i krajnje tačke poslednje stavke nije bitan. Pitanje: Koliko ima takvih spiskova za i) trougao; ii) n-tougao? |