U dvodimenzionalnom koordinatnom sistemu XY jednačina X^2 + Y^2 = 9 je jednačina linije - kružnice.

U trodimenzionalnom koordinatnom sistemu XYZ jednačina X^2 + Y^2 = 9 je jednačina takvih linija za svako Z.
I za Z=0, Z=1, Z=-1, Z=2, Z=1.79....Skup tih beskonačno kružnica čini cilindričnu površ.

Slažem se sa Mikojevim odgovorom. U ravno OXY to je parabola, a u prostoru OXYZ parabolički cilindar.

Hvala na odgovorima!
Umijem zamisliti "kretanja linije" (po nekoj drugoj liniji), "obrtanje linije" (oko tačke ili ose), i tako dobiti "nove geometrijske figure". To sebi "vizuelno osmislim" (kao realno događanje, realno pomjeranje).
Međutim, gledajući slike i date formule, uz čitanje propratnih tekstova, nigdje nisam našao rečenicu: "treću koordinatu odredi po želji" - u skupu realnih brojeva).



_{[Ovu poruku je menjao Sprečo dana 27.07.2011. u 13:51 GMT+1]}

Dobra ti je knjiga. Ako se ne varam Viša matematika, Vigodski???

Jeste Vigodski. Nego slabo se snalazim sa ovim (pozajmljenim) skenerom i postavljanjem odgovarajućih slika. Sve mislim da je korisnije postaviti čitavu stranicu teksta nego samo "izrezati dio".
Temu sam otvorio (uglavnom) zbog opšte jednačine konusnih presjeka:


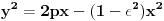
i ove pribilješke (olovkom davno napisane) na strani 75. Radi se o žižnom parametru elipse kojoj je:
a - velika poluosa, b - mala poluosa i 2p = 2b^2/a "žižni parametar".



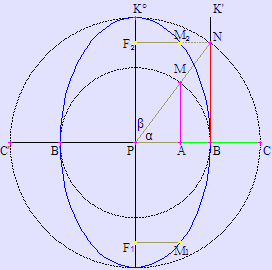Pitanje: Da li je žižni poluparametar za elipsu ?!
Dobro, ne piše to u svakom udžbeniku (da jeste)! To je samo "pripremno pitanje" za sljedeće:
Kako (najlakše, najjednostavnije) konstruisati tu dužinu: 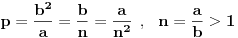, za date poluose elipse a i b ?







_{[Ovu poruku je menjao Sprečo dana 28.07.2011. u 06:12 GMT+1]}

Konkretni sadržaji primjene žižnog poluparametra (p) elipse su "preširoki". Zato nije "bezazleno pitanje":
Da li je, naprimjer na sljedećem crtežu, poluparametar p = PA ?! 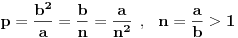. Velika osa elipse je 2a = CC' i mala osa elipse je 2b = BB'.


Treba li objašnjaviti konstrukciju?

_{[Ovu poruku je menjao Sprečo dana 28.07.2011. u 14:52 GMT+1]}

Ne postoji takvo ograničenje koje pominješ. Verovatno ti je rezolucija ekrana relativno niska, pa ne vidiš dugmiće — probaj da se pomeriš udesno.

Ako hoćeš da naučiš i razumeš, nabavi knjigu APSEN III.
Ako hoćeš da nas zaluđuješ, onda pitaj?

Aman, iz Apsena se ne može ništa razumeti, što je dokazano na [es].

@miki069, rečenice ( razmišljanja i iskazi) koje u sebi sadrže: „ako....., onda je....“
- poželjne su ukoliko se odnose na konkretno napisan (postan) sadržaj, uz neko jasno i nedvosmisleno pitanje;
- nisu poželjne ukoliko se odnose na pretpostavljeni sadržaj koji nije naveden u postu i ne odnosi se na konkretno pitanje o kojem se govori.
Tvoja pretpostavka („ako hoćeš da naučiš i razumeš“) nije sadržaj koji se odnosi na prethodno pitanje.
Druga tvoja pretpostavka („ako hoćeš da nas izluđuješ“...onda....“) – je nekorektna!
Molim te, govori u svoje ime („ako hoćeš da me izluđuješ“ – neću da te „izluđujem“, nije mi to namjera).
Postavio sam konkretno pitanje: Da li je, naprimjer na sljedećem crtežu, poluparametar p = PA ?!
Mogao si pitanje ignorisati, odgovoriti sa DA/NE, uz obrazloženje ili bez obrazloženja.
Tvoj takav post, već je inicirao Nedeljkov post i moj odgovor koji nisu u skladu sa postavljenom temom i nisu poželjni.
Predlažem dva rješenja:
Da sam promijeniš post, ili da ti ga moderator pobriše. U oba slučaja treba pobrisati i moj (ovaj) i Nedeljkov post. Je li prijedlog korektan i smislen?
Da i ja predpostavim: Vjerovatno te „izluđuje“ to što nemožeš dokučiti cilj i svrhu tog postavljenog pitanja (a „kopka te“)?! Ne opterećuj se onim što nije navedeno (napisano) i, ako možeš i hoćeš, piši samo o napisanom sadržaju. Ako želiš da ga pojasnim – pitaj!

Stvarno me ne zanimaju žižni poluparametri elipse i ništa me tu ne kopka.
Odgovor se nije odnosio na elipsu, već na tvoju opasku:

"Međutim, gledajući slike i date formule, uz čitanje propratnih tekstova, nigdje nisam našao rečenicu:
"treću koordinatu odredi po želji" - u skupu realnih brojeva)."

Postavio si pitanje, dobio odgovor, ali ti i dalje sumnjaš, jer to u toj knjizi nigde ne piše.
Ako to u toj knjizi ne piše, onda ta knjiga ne valja.
Ako iz te knjige ne možeš razumeti šta u prostoru predstavlja jednačina: Z=3 onda je baci.
Preporučio sam ti koju knjigu da nabaviš da bi razumeo.

U prostoru jednačina 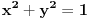predstavlja skup svih tačaka 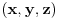tako da je 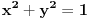. Odatle naravno sledi da pripadanje tačke tom skupu ne zavisi od njene -koordinate, pa pisalo to tako u knjizi ili ne. Ne vidim šta je tu sporno.

Repu mu njegovu, ja pomislio da smo prvo pitanje "adaktirali"!
Hajde, onda, da u okviru tog prvog pitanja postavim sljedeće:
Vjerovatno i vi razlikujete skup tačaka ravni koji nazivamo - a) kružnica, i skup tačaka ravni koji nazivamo - b) krug.
Kako glasi "agebarski zapis geometrijskog opisa" skupa tačaka pod a) , a kako glasi "algebarski zapis geometrijskog opisa" skupa tačaka pod b)?!
Ja jesam "cjepidlaka", i smeta mi kada neko postavi jednačinu kružnice i kaže to je jednačina kruga!

Moj profesor osnova geometrije Zoran Lučić je koristio izraze "krug" za skup tačaka u ravni sa jednačinom oblika

, ,

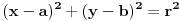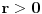odnosno "kružna površ", koja može biti otvorena, kada joj je algebarski oblik

, ,

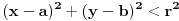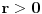odnosno zatvorena, kada joj je algebarski oblik

, .

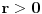Sve je dato u ravni 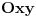. E, sad, on nije koristio ove definicije, jer je kurs bio koncipiran aksiomatski, a ne analitički, ali to već nema veze sa tvojim pitanjem.

Moj profesor je koristio izraze "kružnica" za ono što je Nedeljko označio kao krug, a "krug" ono što je Nedeljku kružna površ, ali je, takođe, naglašavao da je to stvar dogovora i da ne treba insistirati na razlici tih pojmova, jer kod drugih ravnih likova ne insistiramo na tome, nego iz konteksta zadatka znamo o čemu je reč.

Nije ni meni "o glavu" (ali volim što bolji i što precizniji iskaz). "Problem" mi je nastao u jednoj drugoj oblasti u kojoj su tačke poprimile sasvim drugi smisao ("događaji") i gdje se jednačine koriste ka "bogomdane istine" ( ne ulazeći u logiku tih istih algebarskih iskaza).
Volio bih više preciznosti i još više logike u matematičkim (algebarskim) iskazima. Površine su odlična veza izmeđi linija i prostora. Zapazio sam u matematici i previše "konvencija" (dogovorenih značenja, a može i drugačije).
Sviđa mi se Lučićevo "dodavanje", dopuna algebarskog zapisa. To je bolje nego kod nekih autora - "podrazumijeva se"!