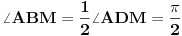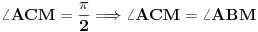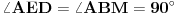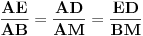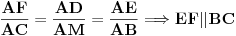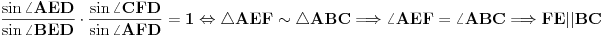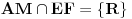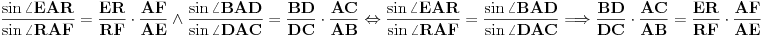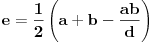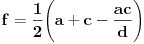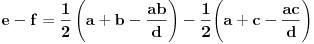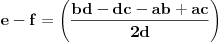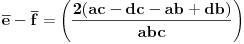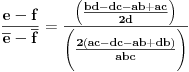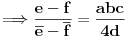[ edisnp @ 29.07.2011. 14:19 ] @
|
| Neka je AM precnik kruga opisanog oko trougla ABC i neka taj precnik sece stranicu BC u tacki D.Ako su E i F podnozja normala iz D na stranicu AB ,odnosno AC,dokazati da je EF||BC.
Kako da rijesim zadatak Primjenom kompleksnih brojeva,na razne nacine pokusavam ali mi ne ide sve se vrtim u krug.Znam da i ako se ovakva metoda zbog icega izbegava to je zbog dosadnog racuna,al meni ne treba cijelo rjesenje nego samo neke smjernice kako da dodjem do rjesenja. |
[ kaćunčica @ 29.07.2011. 15:47 ] @
Geometrijsko rešenje je krajnje jednostavno: uglovi ABM i ACM su uglovi nad prečnikom, pa su pravi, a onda iz sličnosti trouglova AED i ABM, kao i ADF i AMC, sledi da je AE:AB=AD:AM=AF:AC, pa odatle imamo paralelnost traženih pravih.
[ edisnp @ 29.07.2011. 19:50 ] @
Znam takvo rjesenje ali mi je potrebna pomoc oko pirmjene kompleksnih brojeva.Evo ih tri rjesenja zadatka.
1 Nacin
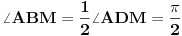
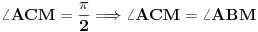
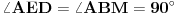
,
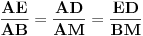
,
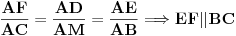
,poslednje je slijedilo iz obrnute Talesove teoreme.
2 Nacin Moze se direktno pokazati primjenom Cevine teoreme
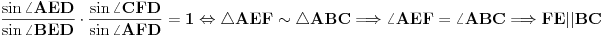
.
3 Nacin Neka je
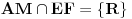
,zakljucak slijedi i iz
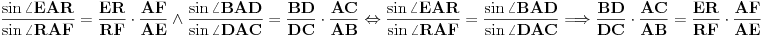
[ Nedeljko @ 31.07.2011. 11:36 ] @
Svako vektorsko planimetrijsko izvođenje se može preformulisati kao kompleksno.
[ edisnp @ 31.07.2011. 12:48 ] @
Moze jos malo pojasnjenja?
[ Nedeljko @ 31.07.2011. 17:58 ] @
z=a+ib ili z=(a,b) za kompleksno z i realne a i b.
Probaj zadatak da rešiš analitički.
[ edisnp @ 01.08.2011. 11:47 ] @
Moze li da se napise:
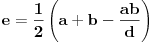
i
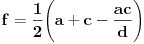
[ edisnp @ 02.08.2011. 13:28 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.