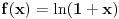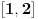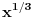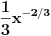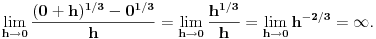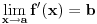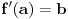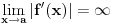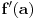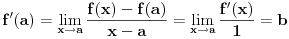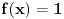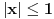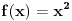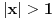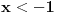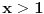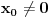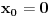[ BlaziX @ 12.08.2011. 14:29 ] @
|
| postovani forumasi (pre svega matematicari) dobar dan.
Posto spremam ispit iz matematicke analize, pa kako ne bi trosio pare na privatne casove za svaku sitnicu na koju naidjem da mi je nejasna, odlucio sam da otvorim ovu temu, a mozda jos nekom pomogne, primera radi mozda mojim kolegama koji isto spremaju analizu (a hvala bogu ima nas dosta)
pitanja su u okviru teorije izvoda sa jednom i vise promenljivih, trenutno to spremam.
pitanja:
1) najpre bi voleo da mi neko razjasni kakva je razlika izmedju neprekidnosti i uniformne neprekidnost, kako se ispituje uniformna neprekidnost kad dobijemo zadatu funkciju, evo primera radi: ispitati jel funkcija f(x)=ln(1+x) uniformno neprekidna nad intervalom [1,2]?
2) -ispitati jer f(x)=x^1/3 (treci koren iz x) diferencijabilna za svako x pripada R | kako se ispituje diferencijabilnost funkcije?
- evo jos jednog tipicno slicnog primera, ispitati z=x^2-xy+y^2 je diferencijabilna za svako x pripada R^2
3)f(x)=(1/2)sin2x+(1/30)sin30x+(1/100)sin100x je diferencijabilna za svako x i jednacin cos2x+cos30x+cos100x=0 ima bar jedno resenje nad intervalom (0,3pi)
4) funkcija z=f(x,y)= -> (xy^2)/(x^2+y^2) , za (x,y razlicito (sad ne znam kako da napisem znak za nejednakost) od (0,0)
-> 0 , za (x,y) = (0,0) , ima parcijalne izvode dz/dx i dz/dz u tacki O(0,0) (upotrebio sam oznaku d za oznacavanje parcijalnih izvoda, nisa znao koju drugu oznaku da upotrebim
ovo su neka od pitanja koja ne razume (ili ne znam kako se resava), u nadi da cete mi pomoci zahvalio bih vam se.. |
[ Nedeljko @ 12.08.2011. 15:04 ] @
1) Svaka ravnomerno neprekidna funkcija na nekom skupu je neprekidna na tom skupu. Obrat u opštem slučaju važi, ali postoji Kantorova teorema o ravnomernoj neprekidnosti po kojoj je svaka neprekidna funkcija na kompaktnom skupu ravnomerno neprekidna na njemu. Obzirom da je 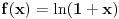 neprekidna funkcija na kompaktnom skupu 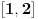 , ona je i ragvnomerno neprekidna na njemu. Primer neprekidne funkcije koja nije ravnomerno neprekidna je 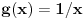 .
2) Ne znam da li se traži ispitivanje diferencijabilnosti po definiciji ili ne. Ako je odgovor negativan, izvod funkcije 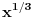 je funkcija 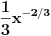 , koja nije definisana u nuli. Nediferencijabilnost u nuli se može dokazati po definiciji.
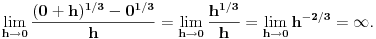
To si mogao da dobiješ na još jedan način: ako postoji konačan 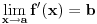 i funkcija  je neprekidna u tački  , onda je funkcija  diferencijabilna u tački  i ima izvod  , tj. 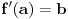 . Isto tako, ako je 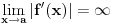 , onda 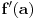 ne postoji. Ovo je neposredna posledica Lopitalovog pravila.
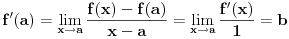 .
Što se diferencijabilnosti funkcija više promenljivih tiče, za diferencijabilnost funkcije u svakoj tački nekog otvorenog skupa dovoljno je da na tom otvorenom skupu postoje parcijalni izvodi te funkcije po svakoj od promenljivih i da su neprekidni na tom otvorenom skupu.
3) Primeni Rolovu teoremu.
4) Nije mi jasno šta je pitanje. [ BlaziX @ 13.08.2011. 09:33 ] @
mnogo hvala, za 4 pitanje sam predpostavio da se nece skontati jel je malo cudno napisano u zbirci (a ne znam kako da napisem) nema veze pitacu kolegu za cetvrto ili cu otici na konsultacije.
[ Nedeljko @ 13.08.2011. 12:16 ] @
Pa, šta je pisalo u zbirci?
[ devetkamp @ 27.11.2012. 13:48 ] @
Jel bi mogao neko da mi pomogne oko dokaza neprekidnosti funkcije y= sin(x) + cos (x) pomocu definicije? Hvala :D
[ Nedeljko @ 27.11.2012. 14:03 ] @
Koristi formule za pretvaranje razlike sinusa i razlike kosinusa u proizvod.
[ devetkamp @ 27.11.2012. 20:39 ] @
Ok. A moze li neko da baci pogled i proveri ovo sto sam pisao...
[ Sonec @ 27.11.2012. 20:53 ] @
Dobro je to.
[ devetkamp @ 29.11.2012. 17:55 ] @
A jel bi neko pogledao ovaj prolem? :D
[ Nedeljko @ 29.11.2012. 18:41 ] @
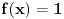 za 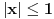 , odnosno 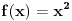 za 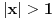 . Koliko se ja razumem, ta funkcija je neprekidna na celom skupu realnih brojeva. [ devetkamp @ 29.11.2012. 19:35 ] @
Mene muci slucaj kad je x<-1, pa onda trazim cemu tezi x^2n .... Jel tacno da taj limes ne postoji? Da li bi bilo isto ako bi umesto x^2n stavili x^n ? hvalaa..
[ Nedeljko @ 29.11.2012. 20:44 ] @
Rekoh da postoji. Funkcija je parna. 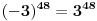 . Za 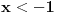 limes je isti kao za 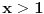 . [ devetkamp @ 30.11.2012. 22:05 ] @
Ok, to mi je jasno... A kad ispitujem neprekidnost funkcije y=cos x , da li razmatram slucaj kada je xo = 0 ?
[ Nedeljko @ 30.11.2012. 23:47 ] @
Dokazuješ neprekidnost u svakoj realnoj tački. Postupak se ne razlikuje.
[ devetkamp @ 01.12.2012. 09:08 ] @
Ok. Da li je u redu dokaz?
[ Nedeljko @ 01.12.2012. 10:15 ] @
Izvođenje koje si naveo za 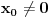 funkcioniše i za 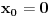 . Ne znam zašto si uopšte razlikovao slučajeve. [ devetkamp @ 01.12.2012. 11:26 ] @
Na vezbama smo tako radili za sin x... sto je izgleda bespotrebno...
[ devetkamp @ 02.12.2012. 17:50 ] @
Jel moze neko da mi pomogne oko zadatka.... Sta dalje??
[ Sonec @ 02.12.2012. 18:08 ] @
Pa nzm, valjda treba da proveris neprekidnost. Sve si tezi na laksi slucaj, sad ne bi trebalo da bude problema.
[ devetkamp @ 02.12.2012. 19:09 ] @
I dalje nisam siguran sta treba da ispisem....
[ Sonec @ 02.12.2012. 19:39 ] @
Aj skiciraj novodobijenu (mada je to ista ta pocetna) funkciju. Videces sam koje tacke su sumnjive da u njima funkcija moze da ima prekid.
[ devetkamp @ 02.12.2012. 21:30 ] @
Zar to nisu bas tacke x=k*pi... ? Ne znam kako da formulisem dokaz o neprekidnosti ( prekidnosti) ?
[ Nedeljko @ 02.12.2012. 21:36 ] @
Da li je funkcija neprekidna u tački 0? A u tački 1? Probaj sa definicijom neprekidnosti.
[ devetkamp @ 02.12.2012. 21:44 ] @
Po definiciji neprekidnosti, levi i desni limes funkcije, kada npr x tezi 1, moraju da se poklope sa vrednoscu funkcije u toj tacki... Ali ja ne znam da ih nadjem, sta je ovde levo a sta desno? Funkcija se sastoji od tacaka, ako se ne varam?
[ Nedeljko @ 02.12.2012. 22:01 ] @
Levo od tačke 5 su svi realni brojevi manji od 5, a desno od broja 5 su svi realni brojevi koji su veći od 5. Koliko je f(1)? Koliko je f(x) kada je x malo manje od 1? A kada je malo veće od 1?
[ devetkamp @ 02.12.2012. 22:15 ] @
Malo sam bolje nacrtao grafik. Funkcija jeste neprekidna u tacki x=1... A u tacki x=0 postoji prekid. Jel tako?
[ Nedeljko @ 02.12.2012. 22:43 ] @
Jeste.
[ devetkamp @ 03.12.2012. 14:33 ] @
Da li je moguce izvesti ovakav zakljucak iz 3. uslova? Da li postoji ovaj limes?
[ darkosos @ 04.12.2012. 08:57 ] @
Nula je nula, nema tu 0+ i 0-. Ako si dobro racunao, to nije tacka prekida. Zamisli da si radio f(x)=x, sta bi dobio u nuli?
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|