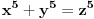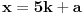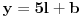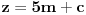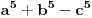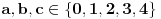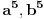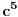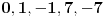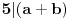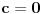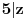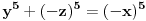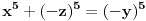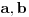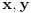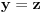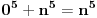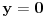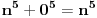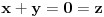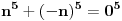[ Teoreticar @ 16.08.2011. 08:50 ] @
|
[ Nedeljko @ 16.08.2011. 09:44 ] @
[ Nedeljko @ 16.08.2011. 14:12 ] @
[ zzzz @ 16.08.2011. 15:34 ] @
Citat: Teoreticar: Nikako mi ne uspijeva da dokazem sledeću tvrdnju: Ako su x, y i z cijeli brojevi i ako vrijedi 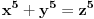 tada su x, y i z djeljivi sa 5. tada su x, y i z djeljivi sa 5.Ako uzmeš x=2, y=-2 i z=0 imaš 32-32=0.I odatle zaključimo da je 32 djeljivo sa pet,ali ostatak pri djeljenju nije nula već je 2.Nešto tu nije jasno. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|