Programerski, data je funkcija
Code:
bool p();
koja ima uvek istu raspodelu kod koje obe vrednosti imaju pozitivnu verovatnoću i čiji su pozivi međusobno nezavisni. Pomoću nje treba realizovati preostale funkcije. Evo koda.
Code:
bool p();
bool coin()
{
bool x, y;
do {
x = p();
y = p();
} while (x == y);
return x;
}
int dice()
{
int result;
do {
result = coin() | (coin() << 1) | (coin() << 2);
} while (result > 5);
return ++result;
}
bool arbitrary(double probability)
{
while (true) {
if (probability >= 1) {
return true;
}
if (probability <= 0) {
return false;
}
if (probability < 0.5) {
if (coin()) {
return false;
}
} else {
if (coin()) {
return true;
}
probability -= 0.5;
}
probability *= 2;
}
}
1. Rešenje pripada fon Nojmanu. Bacamo novćić po dva puta sve dok ne padnu različite vrednosti, a onda smatramo da je eksperiment uspeo ako je prva vrednost pismo. Primer:
PP
PP
GG
PP
GG
GP
Obzirom da je prva vrednost u GP jednaka G, eksperiment nije uspeo. Dokaz se zasniva na činjenici da su događaju PG i GP jednakoverovatni.
2. Koristimo fer novčić koji smo napravili u prvom zadatku. Bacamo ga tri puta da bismo dobili jednu od 8 jednakoverovatnih mogućnosti, koje obeležavamo brojevima od 1 do 8. Postupak ponavljamo sve dok dobijamo brojeve iz skupa {7,8}. Prvi put kada dobijemo vrednost iz skupa {1,...,6}, vraćamo je kao reziltat.
3. Bacamo fer novčić koji smo napravili u prvom zadatku sve dok ne padne pismo. Događaj
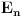
je događaj da je pismo prvi put palo u

-tom bacanju. Ovi događaji su disjunktni, tj. ne može se obistiniti više od jednog i sa verovatnoćom 1 će se obistiniti neki od njih (ne može večito padati glava). Pritom je
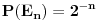
.
Neka je
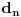

-ta binarna decimala broja

, tj.
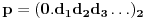
, odnosno
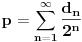
i
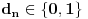
, pri čemu se u nizu
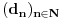
pojavljuje nula beskonačno mnogo puta (nisu sve cifre počev od neke jednake 1).
Neka je
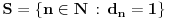
i
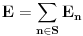
. Važi
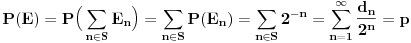
.
Pritom, ako je
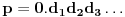
, onda je
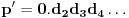
za
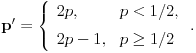
Stoga za niz
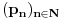
definisan sa
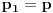
,
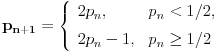
važi
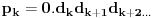
, pa je
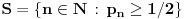
.
[Ovu poruku je menjao Nedeljko dana 19.08.2011. u 22:01 GMT+1]