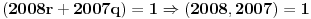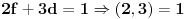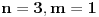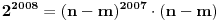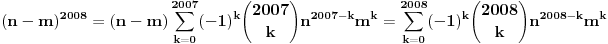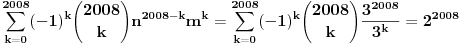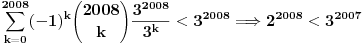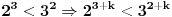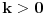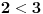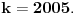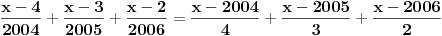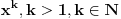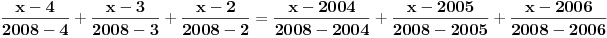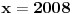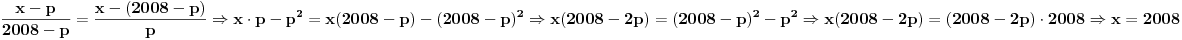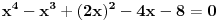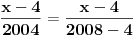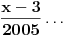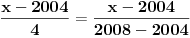[ zmajbk @ 26.08.2011. 19:52 ] @
Evo konkretno radim pripremu za prijemni iz matematike i ovakvi tipovi zadataka mi nikako ne idu. Kod prvog zadatka mi je jasno da moram svesti na iste stepene pa osnova koja je veće taj broj je veći, međutim nikako da to uspijem! Drugi ne znam odakle da krenem :) , a kod trećeg sam brljao sve i svašta. Ako neko zna i ima vremena molio bi da mi ovo razjasni. HVALA 1) Koji je broj 2^2008 i 3^2007 2) (x-4)/2004+(x-3)/2005+(x-2)/2006=(x-2004)/4+(x-2005)/3+(x-2006)/2 3) x^4-x^3+〖2x〗^2-4x-8=0 |