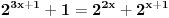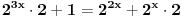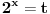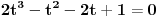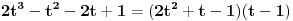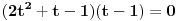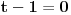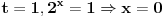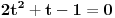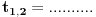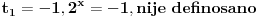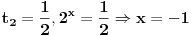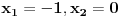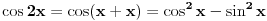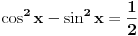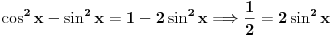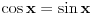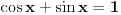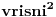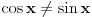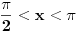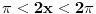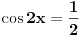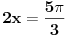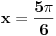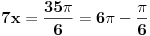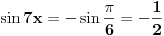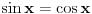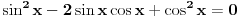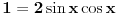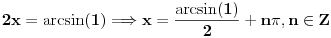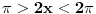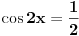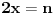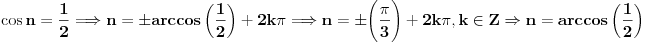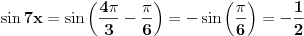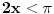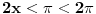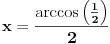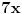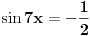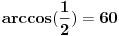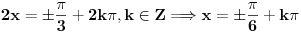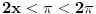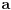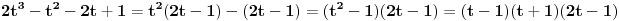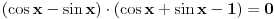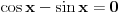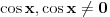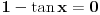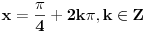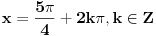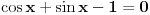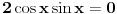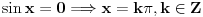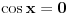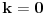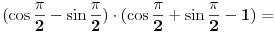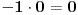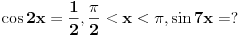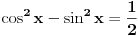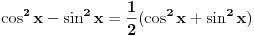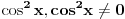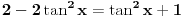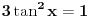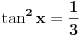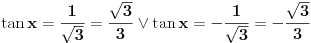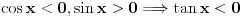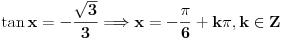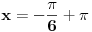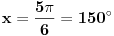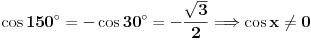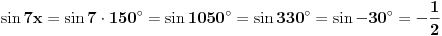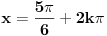[ zmajbk @ 28.08.2011. 20:16 ] @
|
| 1) cos 2x=cos x- sinx
ja ovako rješavam oaj zadatak a sad da li je postupak dobar na vama je da mi ukažete
cos^2x-sin^x=cos x- sinx
(xosx-sinx)(cosx+sinx)=cos x- sinx
e sad da li smijem sve podijeliti sa cos x- sinx (posto postoji mogucnost da je djelilac 0 cosx=sinx za 45° ?????
2) Ako je cos2x=1/2 i , pi/2<x<pi koliko je sin7x
Ovdje me zbunjuje interval pi/2<x<pi posto je cos u tom intervalu negativan?????
3) 2^(3x+1) + 1=2^(2x) + 2^(x+1)
i ovaj me zadatak muči kod eksponen. jednačina. Molim pomoć
Ovo su zadaci sa prijemnog PMF Banja Luka! |
[ Sherlock Holmes @ 28.08.2011. 21:22 ] @
[ edisnp @ 28.08.2011. 21:34 ] @
Evo male pomoci:
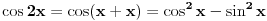 sad kod drugog zadatka imas: 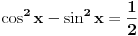
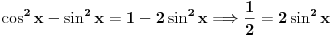 . [ zmajbk @ 28.08.2011. 21:42 ] @
Šta reći nego BRAVO MAJSTORI!
HVALA LJUDI
[ edisnp @ 28.08.2011. 21:46 ] @
A sto se tice prvog zadatka iskoristi isto ono sto sam ti dao u drugo postu dobices dvije jednacine 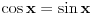 i 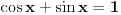 ako bude zapelo nesto vrisni ovdje. [ Sonec @ 28.08.2011. 21:59 ] @
Citat: edisnp: ako bude zapelo nesto vrisni ovdje.
Nije on zensko pa da vrisne, ahahahahahahahahahahaha [ edisnp @ 28.08.2011. 22:05 ] @
Citat: Milan:
Nije on zensko pa da vrisne, ahahahahahahahahahahaha 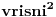 ovdje ovdje[ Sonec @ 28.08.2011. 22:11 ] @
E, super, znas moje ime, pa ti si facafaca.
I nemoj molim te da pises boldiranim slovima, neko ce imati utisak da vices, a to nije lepo da se radi, znas, pogotovo prema starijim osobama.
Nemam sad vremena da se objasnjavam sa tobom, a i nisi vredan toga.
[ edisnp @ 28.08.2011. 22:16 ] @
Evo upravo me je sad jedan clan to zamerio,zbog toga sto si stariji,Ja ne vidim u cemu je problem nista ja protiv tebe nemam,htio sam i ja malo da se nasalim,a sto se tice toga ja nisam vrijedan da se ti raspravljas samnom narano da ne samo ja nego niko nije vrijedan tvog nerviranja niti je iko vrijedan icijeg nerviranja.
[ Nedeljko @ 28.08.2011. 22:55 ] @
U prvom zadatku možeš razlikovati sva slučaja 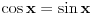 koji rešiš posebno i 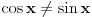 kada možeš skraživati.
U drugom, ako je 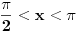 , onda je 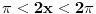 , pa je 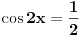 za 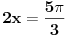 , odnosno 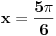 , pa je 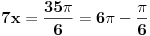 , odakle je 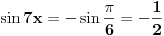 . [ edisnp @ 28.08.2011. 23:09 ] @
[ edisnp @ 29.08.2011. 01:56 ] @
[ zzzz @ 29.08.2011. 09:20 ] @
zmajbk:....(xosx-sinx)(cosx+sinx)=cos x- sinx
e sad da li smijem sve podijeliti sa cos x- sinx (posto postoji mogucnost da je djelilac 0 cosx=sinx za 45° ?????
Ne treba tako razmišljati.Nisi siguran ,a usput bi mogao izgubiti neko rješenje.
Posmatraj ovako:
A*B=A
A*B-A=0
A*(B-1)=0 i odavde izvlačiš dvije jednačine.Ili je A=0 ili B-1=0
Kod tebe je: ili cos x- sinx=0 ili cosx+sinx -1=0
[ Sherlock Holmes @ 29.08.2011. 16:56 ] @
Citat: edisnp: Sad vidoh da se dobije isto rjesenje i za uslov 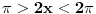 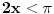 ? [ edisnp @ 29.08.2011. 17:02 ] @
Da 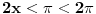 u tom intervalu se dobja isto rjesenje jer je 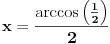 ,ubaci u tu vrijednost za  u 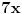 i dobices da je 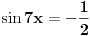 [ Sherlock Holmes @ 29.08.2011. 17:35 ] @
Znam ja vrlo dobro kako se to radi. I, da uprostimo 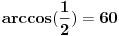 . Moze se ovo resiti na jednostavniji nacin. [ edisnp @ 29.08.2011. 17:42 ] @
Citat: Sherlock Holmes:
Moze se ovo resiti na jednostavniji nacin.
Na primjer. [ Sherlock Holmes @ 29.08.2011. 17:45 ] @
Kasnije cu uraditi decku koji je postavio zadatak. Imam sada obaveza.
[ edisnp @ 29.08.2011. 19:34 ] @
Ovo bi bilo malo prostije: 
Odakle se dobija 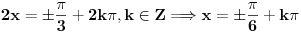 ,u intervalu 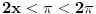 ,kosinus je pozitivan jer je u pitanju prvi kvadrant.I uzima se 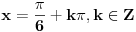 tj, 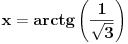 Odakle se lako nalazi 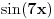 [Ovu poruku je menjao edisnp dana 29.08.2011. u 20:45 GMT+1]
[Ovu poruku je menjao edisnp dana 29.08.2011. u 20:45 GMT+1][ zmajbk @ 29.08.2011. 19:56 ] @
2t^3 - t^2 - 2t + 1 = ( 2t^2 + t - 1 )( t - 1 )
Nije mi oprijatelju jasno kako si dobio ovo na desnoj strani jednačine. Izgleda da meni mnogo klima :)
[ Sherlock Holmes @ 29.08.2011. 20:03 ] @
To sam dobio pomocu Bezuove teoreme. Pogledaj o njoj nesto vise na ovom linku: http://www.matematiranje.com/I...nom_sa_jednom_promenljivom.pdf
Nasao sam nulu polinoma. Neka je 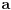 nula polinoma. Tada je taj polinom deljiv sa  . Tako sam podelio polinom treceg stepena na dva polinoma, prvog i drugog stepena koji se veoma lako resavaju. [ Sonec @ 29.08.2011. 20:17 ] @
a moze i ovako, mozda ti je ovako lakse: 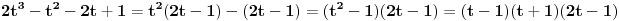 [ zmajbk @ 29.08.2011. 21:09 ] @
Ja sto znam to je HVALA :)
Eto sta se desi kada covjek sa 40 godina hoće da upiše faks (mislim ja imam jednu diplomu fakulteta VISER u džepu) ali slabo mi zarađuje :). A šta ću takva vremena
[ Sherlock Holmes @ 29.08.2011. 22:00 ] @
[ zmajbk @ 29.08.2011. 22:38 ] @
BRAVO, moram biti malo neskroman - tako sam i ja to radio "ranije" prije nekih 15-ak godina ali ispao sam bio totalno iz forme .)
[ Sherlock Holmes @ 30.08.2011. 20:29 ] @
[ zmajbk @ 30.08.2011. 22:34 ] @

Jel može ovako? [ Sonec @ 30.08.2011. 22:53 ] @
Moze, samo bez 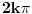 naravno :) [ zmajbk @ 31.08.2011. 13:22 ] @
nego, +??
[ Sonec @ 31.08.2011. 13:54 ] @
Pa ne treba nista dodavati. Jer, da, resenje 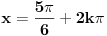 ce biti stalno u drugom kvadrantu, al posto imas i uslov da 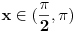 onda uzimas resenje  [ zmajbk @ 31.08.2011. 16:17 ] @
Hehehe učim dok sam živ!
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|