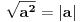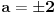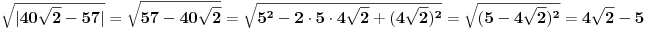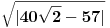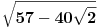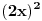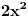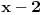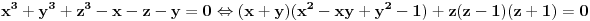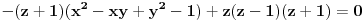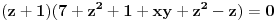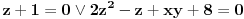[ zmajbk @ 01.09.2011. 14:27 ] @
|
[ Sonec @ 01.09.2011. 14:40 ] @
[ zmajbk @ 01.09.2011. 14:44 ] @
Sorry ali nije mi jasno zasto samo 2 pa moćže ići i 3 na -2
[ Sonec @ 01.09.2011. 14:50 ] @
[ zmajbk @ 01.09.2011. 14:53 ] @
zaboravio sam navesti da rješenje mora biti u skupu cijelih brojeva
[ zmajbk @ 01.09.2011. 14:59 ] @
[ Sonec @ 01.09.2011. 15:04 ] @
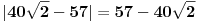 jer je jer je 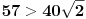 , 57 je malo vece (za jedno 0.4, to sam proverio), al mogla je da se odredjeno vreme vuce ova apsolutna, a ovo sto sam ja uradio je samo jedan deo, pa sam ostavio tebi da resis drugi deo, pa ce se verovatno kada se to sve sredi neke stvari skratiti, a samim tim ce i resenje biti u , 57 je malo vece (za jedno 0.4, to sam proverio), al mogla je da se odredjeno vreme vuce ova apsolutna, a ovo sto sam ja uradio je samo jedan deo, pa sam ostavio tebi da resis drugi deo, pa ce se verovatno kada se to sve sredi neke stvari skratiti, a samim tim ce i resenje biti u 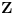 imas ovde za 2. pitanje http://www.elitesecurity.org/t28735-0 [ zmajbk @ 01.09.2011. 15:31 ] @
Pročitao i sad mi je jasno. također i 2. zadatak je jasan (sad :) )
Znaš li šta da radim sa prvim (kako ovaj polinom rastaviti na faktore) ako je to način rješavanja. baš te maltretiram [ Sonec @ 01.09.2011. 15:36 ] @
[ Sherlock Holmes @ 01.09.2011. 15:44 ] @
1.
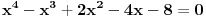 Pomocu Bezuove teoreme mozemo da rastavimo ovaj polinom. Odredimo nulu polinoma 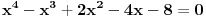 . Nula je . Nula je 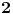 . Prema Bezuovoj teoremi ovaj polinom je deljiv sa . Prema Bezuovoj teoremi ovaj polinom je deljiv sa 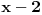 . Podelimo ovaj polinom sa . Podelimo ovaj polinom sa 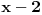 . . 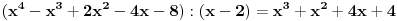 Sada mozemo da rastavimo polinom 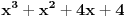 zdruzivanjem. zdruzivanjem. 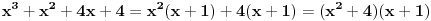 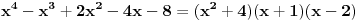 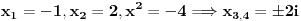 Ako zadatak treba da se resi u skupu realnih brojeva, samo izostavi kompleksno resenje. 2. 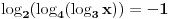 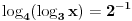 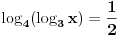 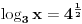 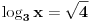 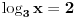 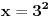 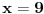 Koren u 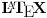 -u kucas "\sqrt{}", samo stavis jos -u kucas "\sqrt{}", samo stavis jos 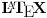 tagove, a potkorenu velicinu kucas izmedju zagrada. tagove, a potkorenu velicinu kucas izmedju zagrada.[ miki069 @ 01.09.2011. 21:18 ] @
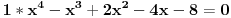 Ako ima racionalnih rešenja oblika p/q onda je p delilac od -8 a q delilac od 1. Kandidati za racionalna rešenja su: 1, -1, 2, -2, 4, -4, 8 i -8. Direktnom zamenom proveriš da jednačinu zadovoljavalju samo X = -1 i X = 2. Polinom je deljiv sa (X+1) i sa (X-2), a pošto su oni uzajmno prosti, onda je deljiv sa njihovim proizvodom. 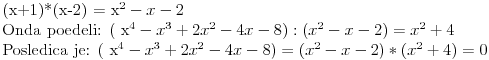 Rešenja su: X1 = -1, X2 = 2, X3 = 2*i, X4 = -2*i, kao i sve njihove permutacije, jer su oni skup rešenja, a ne uređena četvorka. Zadatak za Zmaja za vežbu: Napiši sve četiri Vijetove formule za navedeni polinom i proveri da ih X1, X2, X3 i X4 zadovoljavaju. Zadatak za sve ostale: Rešiti sistem jednačina: 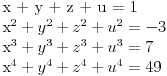 Ako je ovaj težak, može prvo jedan lakši: Rešiti sistem jednačina: 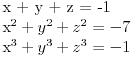 [Ovu poruku je menjao miki069 dana 02.09.2011. u 00:21 GMT+1] [ edisnp @ 02.09.2011. 08:16 ] @
[ miki069 @ 02.09.2011. 12:03 ] @
[ Nedeljko @ 02.09.2011. 14:16 ] @
Ovaj poslednji sistem sam rešio napamet - trojka (x,y,z) je bilo koja od permutacija trojke (2,2,-1).
[ edisnp @ 03.09.2011. 08:42 ] @
Kako ?
[ dejan_m90 @ 03.09.2011. 09:01 ] @
Ma ovaj prvi preko Hornerove sheme....
[ Nedeljko @ 05.09.2011. 07:47 ] @
Da se ispravim, pogodio sam rešenja štimanjem, ali osim toga znam razlog zašto osim tih rešenja nema drugih, tj. da rešenja takvih sistema moraju biti skupovi permutacija jedne trojke.
[ Nedeljko @ 05.09.2011. 07:59 ] @
Inače se takvi sistemi rešavaju onako kako je miki069 rekao. Koristi Njutnove identitete.
Dakle, 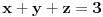 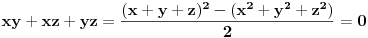 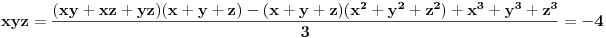 Što znači da je 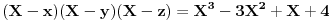 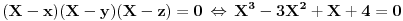 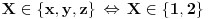 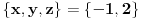 . .E, sad možeš probom da utvrdiš zašto se dvojka mora pojavljivati dvaput, a -1 jedanput. [ miki069 @ 05.09.2011. 10:12 ] @
Upravo kako je Nedeljko napisao i dobro izračunao Vijetove koeficijente iz Njutnovih identiteta.
U zameni je kod X pogrešno prekucao koeficijent 1 umesto izračunate 0. 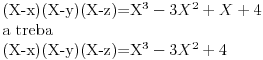 Rešenja x, y i z su u redu. Ovakav sistem vrlo često pada na ispitu iz "Linearne algebre i polinoma" na smeru matematika. Većina profesora i asistenata obrađuje samo Vijetove formule, a Njutnove identitete ni ne spominje. Onda ubace ovo na ispitu i studenti uđu u šumu direktnog rešavanja. Vrlo je teško uraditi bez identiteta koje je Nedeljko naveo. [ edisnp @ 05.09.2011. 18:55 ] @
Ima li neko nesto o Njutnovim identitetima u PDF formatu?
[ Sonec @ 05.09.2011. 19:46 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|