Pošto su u1, u2, u3 ortonormirani vektori onda važi:

u1*u2=0, u1*u3=0, u2*u3 = 0, u1*u1 = 1, u2*u2=1 i u3*u3 = 1.

* mi je oznaka za skalarni proizvod vektrora.


Pretpostavimo suprotno, da su oni linerano zavisni.
Tada bi postojali skalari a, b i c takvi da važi:

(a,b,c)<>(0,0,0) i



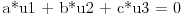
Ovu jednačinu pomnožimo skalarno sa u1 i dobićemo:
a*u1*u1 + b*u2*u1 + c*u3*u1 = 0, to jest
a*1 = 0 odakle sledi a=0.


Istu jednačinu pomnožimo skalarno sa u2 i dobićemo:
a*u1*u2 + b*u2*u2 + c*u3*u2 = 0, to jest
b*1 = 0 odakle sledi b=0.


Istu jednačinu pomnožimo skalarno sa u3 i dobićemo:
a*u1*u3 + b*u2*u3 + c*u3*u3 = 0, to jest
c*1 = 0 odakle sledi c=0.

Dakle dobijamo (a,b,c) = (0,0,0) što je suprotno pretpostavci da je:
(a,b,c)<>(0,0,0).



II način:



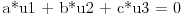
Posle kvadriranja dobija se:



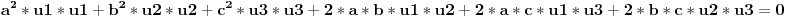
To jest:



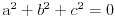
Što je tačno samo ako je: a=0 i b=0 i c=0 i suprotno pretpostavci da je (a,b,c)<>(0,0,0).


<sub>[Ovu poruku je menjao miki069 dana 02.09.2011. u 08:24 GMT+1]

[Ovu poruku je menjao miki069 dana 02.09.2011. u 08:26 GMT+1]</sub>