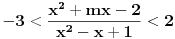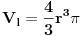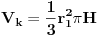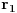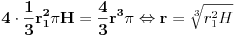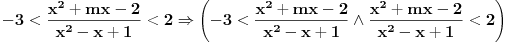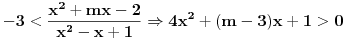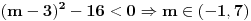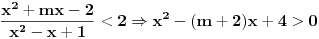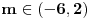[ zmajbk @ 03.09.2011. 10:34 ] @
|
[ edisnp @ 03.09.2011. 11:06 ] @
[ zmajbk @ 03.09.2011. 11:25 ] @
Pa zar poluprečnik lopte nije jednak dvosttrukoj vrijednosti poluprečnika kupe tj. poluprečnk lopte = prečnik kupe
[ zzzz @ 03.09.2011. 11:29 ] @
[ Sonec @ 03.09.2011. 12:28 ] @
[ zmajbk @ 03.09.2011. 12:54 ] @
Molim te možeš mi ovo malo pojasniti kod kvadratne nejednačine. Ja sam to rješavao ovako. razmatram slučaj
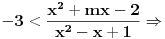 slijedi da je slijedi da je 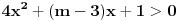 posto je u imeniocu razlomka kvad. jednačina koja je stalno pozitivna, e sad onaj tvoj uslov koji mi nije jasan "Posto je posto je u imeniocu razlomka kvad. jednačina koja je stalno pozitivna, e sad onaj tvoj uslov koji mi nije jasan "Posto je 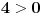 onda slijedi onda slijedi  Zasto D<0 - molim te objasni mi ovo ili daj neki link da dopunim ovo "znanje " iz kv. jednačina i nejednačina Zasto D<0 - molim te objasni mi ovo ili daj neki link da dopunim ovo "znanje " iz kv. jednačina i nejednačina[ kaćunčica @ 03.09.2011. 13:11 ] @
Citat: 3. U jednakostraničnom trouglu stranice a=10 nalazi se 5 tačaka. Dokazati da među tih 5 tačaka postoje dvije čije je rastojanje najviše pet. Podeliš polazni torugao na četiri jednakostranična trougla sa stranicom a/2, tj. 5. Po Dirihleovom principu, bar u jednom od trouglova su dve tačke (nije problem ni ako su na stranicama trouglova) i te dve tačke imaju rastojanje najviše 5. [ Sonec @ 03.09.2011. 13:14 ] @
Ja sam do uslova
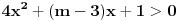 dosao iz nejednacine dosao iz nejednacine 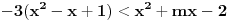 , nekako mi je tako lakse, da ne moram da gledam imenilac i brojilac. , nekako mi je tako lakse, da ne moram da gledam imenilac i brojilac.Sto se tice uslova  pogledaj OVDE. Taj uslov nam govori da ce resenja kvadratne nejednacine biti kompleksni brojevi, tj. da grafik kvadratne f-je nece seci pogledaj OVDE. Taj uslov nam govori da ce resenja kvadratne nejednacine biti kompleksni brojevi, tj. da grafik kvadratne f-je nece seci  osu, a ovo sto sam rekao osu, a ovo sto sam rekao 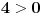 sam rekao jer sam rekao jer 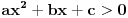 ima resenje kad je ima resenje kad je  (funkcija je konveksna, srecan smajli) i gore spomenuti uslov (funkcija je konveksna, srecan smajli) i gore spomenuti uslov  Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|