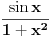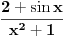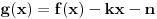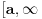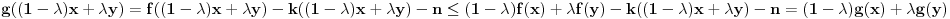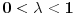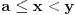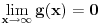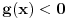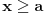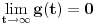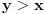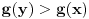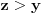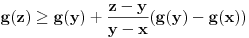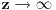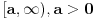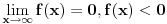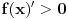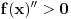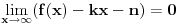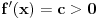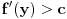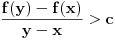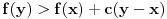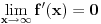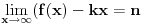|
|
[ nikolinv @ 05.09.2011. 16:10 ] @
|
| Kod osnovnih funkcija koje imaju asimptotu, tipa y=e^x , y=1/x, racionalne funkcije i sl. čiji se tok ispituje u okviru Analize I imamo:
- Ako funkcija prilazi asimptoti odgore, ona je konveksna.
- Ako funkcija prilazi asimptoti odozdo, ona je konkavna.
Ovo je intuitivno sasvim OK, ali kada su asimptote u pitanju, treba biti obazriv sa intuicijom. E sad, moje pitanje je da li neko od vas zna neku funkciju sa asimptotom za koju ovo ne važi, preciznije, da li znate koja funkcija prilazi asimptoti odozgo, a konkavna je? Mislim na funkcuje koje su kombinacija osnovnih (kvadrat, koren, sinus , ln, eksponent ...).
Vrlo dobro se sećam da sam na studijama naišao na ovakvu funkciju, ali prosto nisam poverovao da je to moguće, pa sam tražio gde je greška u drugom (ili prvom izvodu) i nisam je našao. Pošto je to bilo u prošlom veku i nije bilo kompjutera na svakom koraku, nisam mogao da proverim grqafički.
Unapred zahvalan.
|
[ miki069 @ 05.09.2011. 18:46 ] @
Pod asimptote misliš na horizontalne ili kose kada je X dovoljno veliki broj.
Pogledaj geometrijsku definiciju konkavnosti i konveksnosti i biće ti jasno da mora tako da bude kada je X dovoljno veliki.
Funkcija može za konačan broj X-eva da prilazi odozgo konkavno, ali će kad-tad imati prevojnu tačku i početi da bude konveksna.
[ Nedeljko @ 05.09.2011. 22:35 ] @
Funkcija može da ima horizontalnu ili kosu asimptotu, a da nije ni konveksna ni konkavna niti na jednom neograničenom intervalu. Primer takve funkcije je 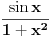 . Međutim, ako znamo da funkcija jeste konveksna, ona horizontalnoj ili kosoj asimptoti (ako je ima) može prilaziti isključivo sa gornje strane. [ nikolinv @ 05.09.2011. 22:48 ] @
Citat: miki069: Pod asimptote misliš na horizontalne ili kose kada je X dovoljno veliki broj.
Pogledaj geometrijsku definiciju konkavnosti i konveksnosti i biće ti jasno da mora tako da bude kada je X dovoljno veliki.
Funkcija može za konačan broj X-eva da prilazi odozgo konkavno, ali će kad-tad imati prevojnu tačku i početi da bude konveksna.
- Mislim i na jedne i na druge asimptote, svejedno je. Lako je od funkcije f koja ima horizontalnu asimptotu dobiti funkciju sa kosom, npr xf, takva funkcija ima sada kosu asimptotu. Slično važi i obrnuto, ako f ima kosu asimptotu y=kx+n, onda će f/k imati horizontalnu. Ne bih hteo da diskusija krene u pravcu asimptota, nego ka konkavnosti.
- I ja sam mislio da će funkcija morati kad-tad da se "nasmeje" (bude konveksna) ako prilazi asimptoti odgore, ali za to nema nekog posebnog argumenta, sem intuitivnog. Pa šta je problem zamisliti takvu neprekidnu funkciju koja nije kompozicija nekih elementarnih funkcija, ništa tu definicija ne smeta. [ miki069 @ 06.09.2011. 08:22 ] @
Konkavno i odozgo na beskonačnom intervalu, ne može. Na konačnom intervalu može.
Ili na beskonačno konačnih intervala može, za šta je lep primer funkcija koju je naveo Nedeljko.
Ima beskonačno prevojnih tačaka.
Pogledaj geometrijsku definiciju (ne posledicu da je drugi izvod <> 0) konkavnosti (konveksnosti) na konačnom intervalu,
zatim tu definiciju proširi na beskonačan interval i biće jasno.
Ako treba dokaz uradiću.
[ Nedeljko @ 06.09.2011. 09:08 ] @
Ne, moj primer nije dobar. Trebalo je 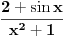 . [ nikolinv @ 06.09.2011. 09:43 ] @
Ne mislim na takvu vrstu funkcije, nego na funkciju tipa y=1/x za x>0 koja ima asimptotu y=0,veća je od nule, samo da joj drugi izvod izvod počevši od nekog a>0 bude negativan. Znači kao y=1/x samo da joj je drugi izod negativan. Tangenta treba stalno da pada, a da f'>0. Nema tu po meni ništa sporno, pa kako vrednost te iste funkcije 1/x stalno pada, a nikad nije negativna, isto tako da se ponaša i njena tangenta, odnosno njen prvi izvod.
[ Nedeljko @ 06.09.2011. 09:59 ] @
Citat: nikolinv: Lako je od funkcije f koja ima horizontalnu asimptotu dobiti funkciju sa kosom, npr xf, takva funkcija ima sada kosu asimptotu. Slično važi i obrnuto, ako f ima kosu asimptotu y=kx+n, onda će f/k imati horizontalnu.
Mala omaška. Treba f+x, odnosno f-kx.
Pretpostavimo da je  definisana i konveksna funkcija na intervalu 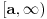 za koju je 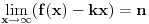 .
Neka je 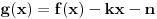 . Funkcija  je takođe konveksna na intervalu 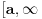 To sledi iz
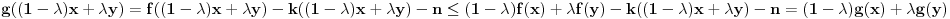 .
Naravno, tu je 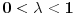 i 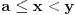 .
Pritom je 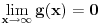 .
Pretpostavimo da je 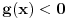 za neko 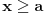 . Zbog 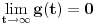 mora postojati neko 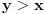 takvo da je 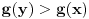 . Za svako 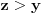 važi
 ,
odnosno 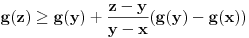 .
Pusti da 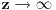 i dobijaš kontradikciju sa uslovom 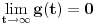 .
[Ovu poruku je menjao Nedeljko dana 06.09.2011. u 16:43 GMT+1][ Nedeljko @ 06.09.2011. 10:06 ] @
Moj primer pokazuje da funkcija može kosoj ili horizontalnoj asimptoti da prilazi sa jedne strane, a da ne bude ni konveksna ni konkavna ni na jednom beskonačnom intervalu.
[ nikolinv @ 06.09.2011. 13:28 ] @
Negde piše da je svaki dokaz akt ubeđivanja. Ako je to tako onda me nisi baš ubedio, Nedeljko. Hajde da malo uprostimo i formalizujemo ovaj problem:
Da li postoji funkcija f na intervalu 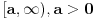 potreban broj puta diferencijabilna i neprekidna, za koju važi:
a) 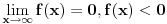
b) 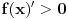
c) 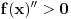
Ako pogledamo sada tvoj dokaz sa ovakvim pretpostavkama, tu bi parametri k i n bili nula tj. važilo bi f = g, tako da nemamo nikakvu kontradikciju sa uslovom 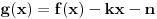 . Molio bih da se dalja diskusija, ako je bude, ograniči na uslove a) b) i c) zbog jednostavnosti, lako je posle problem "zakositi" ili "podići". Znači, govorimo o stalno rastućoj funkciji manjoj od nule koja za asimptotu ima x osu. Da li njen drugi izvod na intervalu 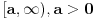 može biti uvek veći od nule počevši od nekog a ili ne može? [ Nedeljko @ 06.09.2011. 15:55 ] @
Izvinjavam se, potkrala se greška an samom kraju. Ispravljeno je. No, krajnje je nebitno koliko su  i  .
Ja sam koristio definiciju konveksnosti i dokazao da se ne mogu istovremeno zadovoljniti uslovi
1. Funkcija  je definisana i konveksna na intervalu 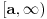 ,
2. 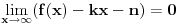 .
3.  za bar jedno 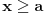 .
Ne znam šta imaš protiv definicije konveksnosti. Naravno da taj uslov sledi iz pozitivnosti drugog izvoda, ali da bi funkcija bila konveksna nije neophodno da bude diferencijabilna. Ovo što ti tražiš je samo specijalan slučaj onoga što sam već dokazao. Uslov sa prvim izvodom nije bitan.
No, može i tako. Ako je 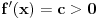 za bar jedno  , onda je 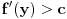 za sve 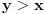 (zbog pozitivnosti drugog izvoda). No, onda po Lagranževoj teoremi o srednjoj vrednosti mora biti 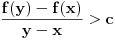 za svako 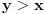 , odnosno 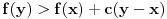 , što znači da funkcija ode u beskonačnost, pa ne može težiti nuli.
Ipak bih ti savetovao da proučiš dokaz opšteg slučaja. [ nikolinv @ 07.09.2011. 13:37 ] @
Priznajem, nisam bio u pravu. Nemojte nikada potceniti moć sopstvene zablude.
Rešenje preko funkcije prvog izvoda. Koristiću onaj slučaj za koji važi a), b) i c) (videti niže):
1. Da bi funkcija prišla asimptoti oddole, mora da bude rastuća, tj f' mora biti pozitivan, počevši od nekog a.
2. Kako se funkcija f u beskonačnosti "pretvara" u x - osu, mora njen prvi izvod težiti nuli, 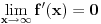 .
3. Konačno, drugi izvod, izvod funkcije f', je veći od nule, pa funkcija f' koja je pozitivna (videti 1.) stalno raste i ne dozvoljava funkciji f' da teži nuli.
Drugi način dokazivanja (Nedeljkov) bi bio da se ospori ograničenost ovakve funkcije.
Zaključak: Ako neka npr. materijalna tačka treba da se u beskonačnosti zaustavi, ne može da ubrzava, nego mora da se koči (logično?!).
Pozdrav svima. [ kaćunčica @ 07.09.2011. 15:37 ] @
^ zanemarujete opciju minus beskonačno, zanemarujete opadajuće kose asimptote... ovi zaključci ne odnose se na sve slučajeve
[ Nedeljko @ 07.09.2011. 16:31 ] @
Nisam zanemario ništa. Kakvi god da su  i  iz 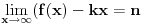 sledi 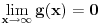 . Kosa asimptota prelazi u horizontalnu, a konveksnost i strana sa koje se prilazi su očuvane. [ kaćunčica @ 07.09.2011. 23:40 ] @
Citat: kaćunčica: ^ zanemarujete opciju minus beskonačno, zanemarujete opadajuće kose asimptote... ovi zaključci ne odnose se na sve slučajeve
Mislila sam na zakljucke:
Citat:
1. Da bi funkcija prišla asimptoti oddole, mora da bude rastuća, tj f' mora biti pozitivan, počevši od nekog a.
2. Kako se funkcija f u beskonačnosti "pretvara" u x - osu, mora njen prvi izvod težiti nuli, .
3. Konačno, drugi izvod, izvod funkcije f', je veći od nule, pa funkcija f' koja je pozitivna (videti 1.) stalno raste i ne dozvoljava funkciji f' da teži nuli.
a "zanemarujete" je bilo persiranje, a ne množina. [ Nedeljko @ 08.09.2011. 08:58 ] @
Pa, opšti slučaj je sveden na slučaj horizontalne asimptote koja se poklapa sa x-osom. Stoga je samo taj slučaj razmatran.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|