[ kompleksna @ 06.09.2011. 12:45 ] @
| kako da nadjem poluprecnik luka u 3d ako su mi poznate tri tacke, pocetna (x1, y1, z1), krajnja (x3, y3, z3) i srednja (x2, y2, z2) koja je tacno na sredini izmedju prethodne dve? hvala |
|
[ kompleksna @ 06.09.2011. 12:45 ] @
[ Nedeljko @ 06.09.2011. 13:09 ] @
[ kompleksna @ 06.09.2011. 14:03 ] @
ok, hvala!
a mogu li sada naci koordinate centra te opisane kruznice? [ darkosos @ 06.09.2011. 14:24 ] @
Ako ti je ovo zadatak analiticke geometrije, onda bi generalni pristup bio:
jednacinom tacaka koje su jednako udaljene od A i B dobijas njihovu simetralnu ravan npr. alfa jednacinom tacaka koje su jednako udaljene od B i C dobijas njihovu simetralnu ravan npr. beta u preseku ove dve ravni dobijas npr pravu p koja u preseku sa ravni ABC daje taj centar kruga tim pristupom mozes doci i naknadno do poluprecnika [ kompleksna @ 07.09.2011. 09:00 ] @
a kako se to radi?
[ darkosos @ 07.09.2011. 10:00 ] @
A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3)
d(X, A) = d(X, B) 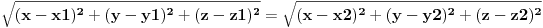 Posle sredjivanja dobices linearnu jednacinu po x, y i z, koja zapravo predstavlja pomenutu simetralnu ravan. Pa onda isto to za d(X, B) = d(X, C) Pa onda presek dve ravni: http://en.wikipedia.org/wiki/P...ntersection_between_two_planes Pa onda presek dobijene prave i ravni ABC: http://en.wikipedia.org/wiki/P...e_a_plane_through_three_points http://en.wikipedia.org/wiki/Plane-line_intersection [ Nedeljko @ 07.09.2011. 11:17 ] @
[ kompleksna @ 08.09.2011. 08:57 ] @
Nadjoh vektore normala ravni:
(n_1 ) ⃗=(A_1,B_1,C_1) gde su 〖 A〗_1= x_2-x_1, B_1= y_2-y_1, C_1= z_2-z_1 (n_2 ) ⃗=(A_2,B_2,C_2) gde su 〖 A〗_2= x_3-x_2, B_2= y_3-y_2, C_1= z_3-z_2 Ravni se seku op pravoj čiji je vektor pravca (n_1 ) ⃗×(n_2 ) ⃗ Nadjoh da je vektor pravca prave p ⃗=(a,b,c) gde su a=B_1 C_2-C_1 B_2 , b=C_1 A_2-A_1 C_2 , c=A_1 B_2-B_1 A_2 Sta dalje? Hvala na razumevanju! [ Nedeljko @ 08.09.2011. 09:43 ] @
Pa, ništa, izaberi slobodan član u jednačini tako da prođe kroz bar jednu od tih tačaka, pa će proći i kroz ostale dve ako ima odgovarajući vektor normale.
[ kompleksna @ 08.09.2011. 09:57 ] @
Da li to znaci da za slobodan clan mogu uzeti jednu od tri zadate tacke?
[ Nedeljko @ 08.09.2011. 11:14 ] @
Da bi ravan
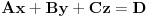 sadržala tačku sadržala tačku 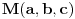 , potrebno je i dovoljno da bude , potrebno je i dovoljno da bude 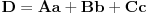 . Ako na to misliš, onda da. . Ako na to misliš, onda da.Može i kraće. Neka je  tražena tačka, tražena tačka, 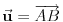 , , 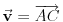 i i 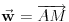 . Kako tačka . Kako tačka  leži u ravni određenoj tačkama leži u ravni određenoj tačkama  , ,  i i  , postojaće neki realni brojevi , postojaće neki realni brojevi  i i  takvi da je takvi da je 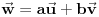 . Sređivanjem jednačina . Sređivanjem jednačina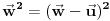 , ,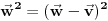 , ,dobija se sistem od dve linearne jednačine sa dve nepoznate  i i  (voditi računa o tome da na mora biti (voditi računa o tome da na mora biti 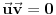 ). Njegovim rešavanjem se dobija tražena tačka ). Njegovim rešavanjem se dobija tražena tačka  . .Ovaj metod je primenljiv u prostoru sa bilo kojim brojem dimenzija ne manjim od dva. [ kompleksna @ 08.09.2011. 13:31 ] @
Pozdrav!
Interesuje me kako da sredim ovaj sistem kada imam i nepoznate a i b, a i koordinate tacke M su mi nepoznate. Da li bi ovaj pristup mogao da se koristi i za nalazenje centra kruznice ili sfere ukoliko su poznate bilo koje tri tacke? [ darkosos @ 08.09.2011. 14:21 ] @
[ kompleksna @ 09.09.2011. 08:57 ] @
Hvala mnogo Nedeljko!
Da li bi ovaj pristup mogao da se koristi i za nalazenje centra kruznice ili sfere ukoliko su poznate bilo koje tri tacke? [ Nedeljko @ 09.09.2011. 09:10 ] @
Pa, ovo i jeste postupak za određivanje centra kruga. Sa druge strane, sfera je određena sa četiri nekomplanarne tačke.
[ kompleksna @ 09.09.2011. 10:51 ] @
Hvala!
Da li postoji nacin da se nadje centar sfere sa samo tri tacke? [ zzzz @ 09.09.2011. 11:08 ] @
Citat: Može čak i sa dvije ako su dijametralno suprotne. [ kompleksna @ 09.09.2011. 11:14 ] @
Koji je najlaksi način da se nadje centar sfere ako su poznate tri tacke na njoj? [ Nedeljko @ 09.09.2011. 12:34 ] @
Trebaju ti 4 tačke, 3 nisu dovoljne.
[ kompleksna @ 09.09.2011. 12:58 ] @
Ok.
Ukoliko imamo 4 tačke, koji je najlakši način da se nađe centar sfere? [ Nedeljko @ 09.09.2011. 13:34 ] @
[ kompleksna @ 12.09.2011. 13:45 ] @
Jasno.
Hvala! [ kompleksna @ 20.09.2011. 08:30 ] @
A kako da nadjem duzinu luka u 3d ako su mi poznate dve tacke, centar luka i poluprecnik?
Mnogo hvala! [ Nedeljko @ 20.09.2011. 09:30 ] @
[ kompleksna @ 20.09.2011. 10:55 ] @
A ukoliko je ugao nekonveksan?
[ kompleksna @ 27.09.2011. 10:25 ] @
Pozdrav!
Poznato: pocetna i krajnja tacka luka (3d), poluprecnik i center luka. Od tacke koja je na luku znam x i y koordinate, kako da nadjem z koordinatu? Hvala! [ kompleksna @ 28.09.2011. 09:37 ] @
A sta ako su mi poznate pocetna i krajnja tacka, poluprecnik, i centar luka sve u 3d
a trazim tacku na luku koja deli luk npr na pola ili na cetvrti deo? unapred hvala! [ kompleksna @ 28.09.2011. 12:52 ] @
Ustvari, da li postoji parametarska j-na kruga (luka) za 3d?
Hvala! Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|