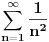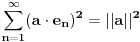[ edisnp @ 10.09.2011. 10:07 ] @
|
[ SrdjanR271 @ 10.09.2011. 13:00 ] @
Citat: edisnp: Kako da dokazem: 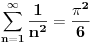 ? ?To je čuveni Bazelski problem, a rešio ga je Leonard Ojler. Originalno Ojlerovo izvođenje polazi od Maklorenovog reda za sinus. 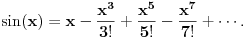 Deljenjem sa 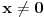 , dalje je , dalje je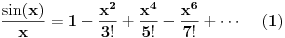 Nule funkcije 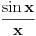 su su 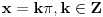 Pretpostavimo sada da možemo ovu funkciju predstaviti kao proizvod linearnih faktora kao kod polinoma. 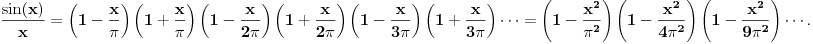 Sada ovaj proizvod formalno izmnožimo samo za članove koji sadrže  i izjednačimo sa koeficijentom uz i izjednačimo sa koeficijentom uz  u (1). u (1).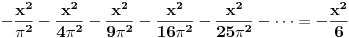 Deljenjem sa  dobijamo: dobijamo: 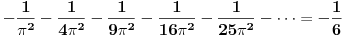 Množenjem sa 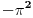 dobijamo: dobijamo: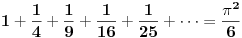 Ovo nije strogi dokaz. Ovde imaš 14 dokaza. [ Nedeljko @ 10.09.2011. 13:20 ] @
Postoji opšti postupak za izračunavanje
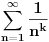 za parno prirodno za parno prirodno  , a koji se zasniva na poređenju razvoja sinusa u beskonačan red (Maklorenova formula) i u beskonačan proizvod (Ojlerovo razlaganje sinusa). , a koji se zasniva na poređenju razvoja sinusa u beskonačan red (Maklorenova formula) i u beskonačan proizvod (Ojlerovo razlaganje sinusa).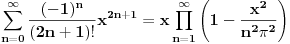 , ,odnosno smenom 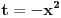 se dobija se dobija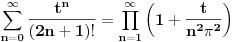 . .To je poređenje razvoja funkcije 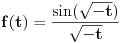 za za 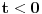 , odnosno , odnosno 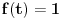 za za 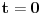 . .No, ovo što tebe zanima može i preko Furijeovih redova. Razvi na intervalu 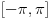 funkciju funkciju 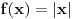 . .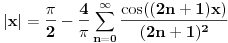 , za , za 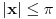 . .Jednakost je tačna zato što je razvijena neprekidna, deo po deo glatka funkcija. Zamenom  sa nulom dobija se da je sa nulom dobija se da je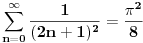 . .Neka je 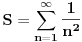 . Obzirom da je . Obzirom da je 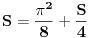 , mora biti , mora biti 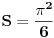 . .Primenom Parsevalove jednakosti na isti Furijeov red može se dokazati da je 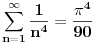 . .[ edisnp @ 10.09.2011. 13:27 ] @
[ edisnp @ 11.09.2011. 18:29 ] @
[ Nedeljko @ 11.09.2011. 22:46 ] @
Pročitaj poslednju rečenicu moje prethodne poruke.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|