Koliko vidim, je oznaka za meru u . Pogledaj definiciju Lebegove mere.

.

Obzirom da je za ,

.

Ja sam skroz pogresio, nije u pitanju Lebegova, vec Zordanova mera (ako moze, nek mod promeni naslov).

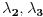
Ja znam sta predstavlja , da je to Zordanova mera, al nije mi (tek sad) jasno sta predstavljaju velicine , da li one imaju veze sa Zordanovom ili Lebegovom merom? Pogledacu definiciju, samo je problem sto mi ovo nismo radili ranije i onda se to odjednom uvodi u dokazu, kao da smo to vec ranije spominjali.

Tacnije, da ne budem neposten prema profesoru, mi smo navodili definiciju koja opisuje zanemarljivost (Lebegova mera nula), neka svojstva zanemarljivosti i jednu Lebegovu teoremu (koju je profesor dokazivao 2 casa). Al nam je rekao da ne moramo to da ucimo, da cemo to uciti kasnije za vreme studija, cak nam je rekao da nismo obavezni da prisustvujemo tom casu kada on to bude radio.

Svejedno. I Žordanova mera ima sva potrebna svojstva za navedeno izvođenje. Lebegova teorema koju je profesor dokazivao je po svoj prilici teorema o Riman-integrabilnosti (funkcija definisana na skupu merljivom po Žordanu je Riman-integrabilna ako i samo ako je ograničena sa skupom tačaka prekida Lebegove mere nula).