Neka je
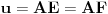
,
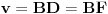
i
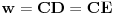
. Jasno je da je
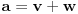
,
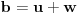
,
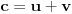
i
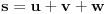
.
Iz
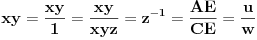
itd. zaključujemo da se jednakost koju treba dokazati svodi na
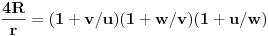
,
odnosno
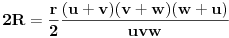
.
Na osnovu prethodnog i sinusne teoreme, to je ekvivalentno sa
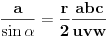
,
odnosno sa
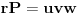
.
Obzirom da je
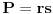
, sledi da je to ekvivalentno sa
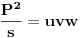
.
Na osnovu Heronovog obrasca, ovo je ekvivalentno sa
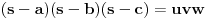
,
a ovo sledi iz jednakosti
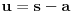
,
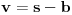
i
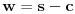
koje se lako dokazuju.