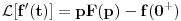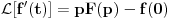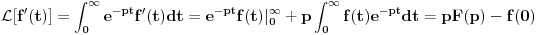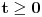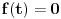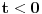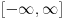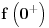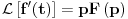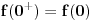Pa, Njutn Lajbnicova formula za Rimanov integral glasi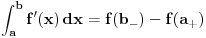

,

ako je podintegralna funkcija definisana i Riman-integrabilna na intervalu 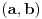i vrednosti na desnoj strani jednakosti postoje.

Mozda zato što je Laplasova transformacija definisana za f(t) za koju vazi

za , odnosno za .

Ili preko Hevisajdove f-je. Zato 0- ne može.

_{[Ovu poruku je menjao SrdjanR271 dana 20.09.2011. u 20:12 GMT+1]}

Na tehnickim fakultetima ce ti reci ovo sto je Srdjan rekao. Ovo je tzv. unilateralna Laplasova transformacija (pretpostavlja se da je funkcija kauzalna, sto je slucaj u svim realnim sistemima).

Postoji i bilateralna Laplasova transformacija (definisana na ) i ona nema clan vec je:

Hteo bih malo detaljnije da ovo prodiskutujemo pa cu dati malo vise teksta oko stvari koje me malo bune.

Laplasova transformacija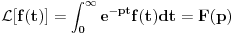



Laplasova transformacija postoji za sve tzv. funkcije eksponencijalnog tipa, tj. funkcije za koje vazi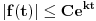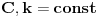





Ja zelim da za takvu funkciju koja uz to ima sve izvode potrazim LT njenog izvoda

Iskoristim definiciju LT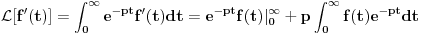



Za ovo razmatranje oko kojeg sam i postavio temu bitan je prvi clan s desne strane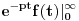



Kako je funkcija 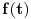eksponencijalnog tipa njena vrednost u gornjoj granici ce biti . Tj. po meni ce biti



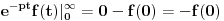U svim nekim diferencijalnim jednacinama koje se rade primenom ove transformacije uzima se zapravo vrednost u nuli i ona je data u pocetnim uslovima. Da li mozes da mi das neki primer kada mi je bitno ovo .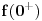

_{[Ovu poruku je menjao petarm dana 01.10.2011. u 15:43 GMT+1]}

Pa, ako je funkcija definisana u nuli i neprekidna sa desne strane. Ne vidim šta je tu sporno.