Valjda Z^2 ima dva puta veći argument od Z.

Z=x + y*i

afiks od 1 tačka P(1,0)
afiks od Z tačka Q(x,y)
afiks od Z^2 tačka R(x^2-y^2,2*x*y)

Ne gubiš puno na opštosti ako uzmeš da je recim kod temena Q prav ugao.
Izračunaj dužine kateta PQ i QR i hipotenuze PR.
Primeni Pitagorinu teoremu, sredi i dobićeš vezu između x i y, to jest geometrijski položaj.
Ako se zapetlja, promeni gde je prav ugao.

da, u pravu si za argument, pogrešno sam otkucao.

probao sam preko analitičke geometrije i jednačine prave kroz dve tačke, primenio uslov normalnosti ali ništa konkretno. Samo se zakomplikuje i to je to.
Zadatak je iz prethodnog ispitnog roka, niko od apsolvenata matematike nije položio. Naravno, zadatak nije bio jedini.

Koristi iz analitičke geometrije udaljenost 2 tačke i koristi Pitagorinu teoremu.
Ja sam probao da je prav ugao afiks od Z i skratili su mi se svi X^4 i Y^4.
Relativno je komplikovan izraz koji je ostao.
Treba ga transformisati, eventualno preći na polarne koordinate da bi se prepoznala kriva linija.
U zadatku nije fiksirano da li je prav ugao u temenu afiksu od 1, z ili z^2
Zameni teme gde je prav ugao.
Možda se dobije prostije ako se uzme da je prav ugao u afiksu od 1 ili Z^2.
Bitno je da dobiješ krivu drugog reda (bez X^3 ili Y^3) i time je zadatak završen.
Ako ne može drugog reda onda polarne koordinate.

Uspeo sam da dobijem nesto preko vektora. Za pocetak pretpostavimo da je pravu ugao izmedju
duzi koja spaja 1 i z i duzi koja spaja 1 i z²

Tada mora biti

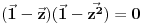
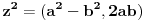
Ako napisemo z=(a,b) i 1=(1,0) onda se dobija i




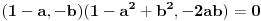
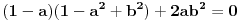
E kad se ovo malo sredi, da ne pisem sve, dobija se a=-1 i proizvoljno b razlicito od nule.
Ima jos resenja ali daju situaciju u kojima je skalarni prozivod nula ali ugao nije prav.

hvala, razmotriću ovo kasnije. već sam bio odustao od ovog zadatka