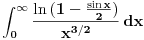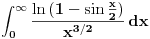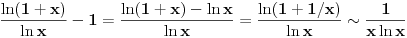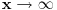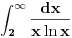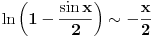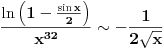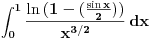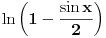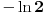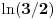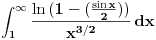[ dukowski @ 30.09.2011. 09:44 ] @
|
| Molim za pomoc oko ispitivanja konvergencije ova dva integrala:
int(0->inf) ( ln(1-(sinx/2)) / (x^(3/2)) ) dx
int(2->inf) ( (ln(x+1)/lnx) - 1 ) dx
Kod prvog, posto je gornja ln funkcija ogranicena na intervalu (-0.693, 0.4) za vrijednosti sin (-1, 1) pokusao sam da stavim da je podintegralna funkcija veca od -1/(x^3/2) pa da dokazem da int -1/(x^3/2) u datim granicama divergira, ali podintegralna funkcija mora biti >0, pa tako rjesenje otpada...
Kod drugog sam pokusao sa reciprocnom vrijednosti lnx/ln(x+1) ali na kraju se pokaze da veca funkcija divergira, sto takodje ne dovodi do rjesenja....
Ako neko ima neku ideju, zamolio bih da je iznese...hvala :)
[Ovu poruku je menjao dukowski dana 30.09.2011. u 10:55 GMT+1] |
[ Nedeljko @ 30.09.2011. 11:24 ] @
Što se prvog tiče, ne znam da li ti treba
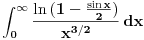
ili
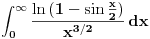
.
Što se drugog tiče,
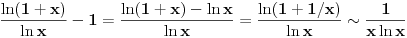
kad
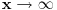
,
pa integral divergira zajedno sa
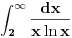
.
[ dukowski @ 30.09.2011. 11:45 ] @
Sto se tice prvog, treba mi za (sinx)/2, tj ova prva opcija...hvala mnogo za ovaj drugi :) nisam se sjetio tablicnog limesa (1+1/x)^x kad x->inf :)
[ Nedeljko @ 30.09.2011. 12:41 ] @
Kada je

blisko nuli, onda je
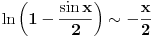
, pa je
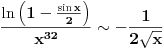
, pa
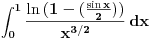
konvergira.
Sa druge strane,
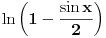
je ograničeno između
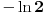
i
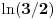
, pa
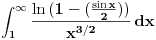
konvergira. Samim tim
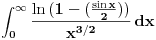
konvergira.
[ dukowski @ 30.09.2011. 12:45 ] @
Super, hvala :)
[ dukowski @ 30.09.2011. 13:01 ] @
Samo jedna sitnica, posto ln(1-(sinx)/2) tezi -x/2, da li podintegralna funkcija moze i smije da bude negativna kao u ovom slucaju da bi integral konvergirao?
[ Nedeljko @ 30.09.2011. 13:52 ] @
Sme. Ovaj integral konvergira apsolutno.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.