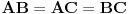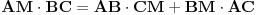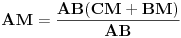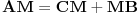Nisam vešta sa LateXom, ali razumećemo se i ovako:
-primeti da je ugao AMC = 60 stepeni
-zarotiraj tačku A oko M za -60 i dobiješ tačku A' na duži MC
-primeti da je trougao AMA' jednakostraničan, tj, AA'=AM
-sada treba pokazati da je A'C=MB, ali to je očigledno jer se one rotacijom oko A za 60 stepeni preslikavaju jedna na drugu (ako više voliš, pokaži podudarnost trouglova AA'C i AMB)
 [Ovu poruku je menjao berazorica dana 01.10.2011. u 07:58 GMT+1]
[Ovu poruku je menjao berazorica dana 01.10.2011. u 08:00 GMT+1]
[Ovu poruku je menjao berazorica dana 01.10.2011. u 07:58 GMT+1]
[Ovu poruku je menjao berazorica dana 01.10.2011. u 08:00 GMT+1]
-zarotirala sam oznake u odnosu na postavku zadatka-
[Ovu poruku je menjao berazorica dana 01.10.2011. u 10:43 GMT+1]