[ dukowski @ 03.10.2011. 09:03 ] @
| Kako rijesiti neodredjeni integral oblika ( sqrt(1+x^4) ) / (1-x^4)? Ne uklapa se ni u jedan od 10-ak tipova neodredjenih integrala koji se pojavljuju u literaturi. |
|
[ dukowski @ 03.10.2011. 09:03 ] @
[ Nedeljko @ 03.10.2011. 09:43 ] @
Izražava se preko hipergeometrijskih funkcija i verovatno ne može kao elementarna funkcija.
[ pexxi92 @ 03.10.2011. 11:55 ] @
Kolko se secam x^2+1/x^2=t bi trebalo da radi...
Javicu se kasnije nemam sad mnogo vremena [ dukowski @ 03.10.2011. 13:19 ] @
Hm...tesko da moze ovom smjenom...u Uscumlicu ima rjesenje za ovaj integral (bez postupka) i sastoji se od elementarnih funkcija...
[ pexxi92 @ 03.10.2011. 13:44 ] @
Ova smena je 100% ako hoces napisacu ti kasnije postupak
[ dukowski @ 03.10.2011. 14:05 ] @
Moze prvih nekoliko koraka ako stignes i ako ti se da...pokusacu i ja u medjuvremenu...
[ pexxi92 @ 03.10.2011. 14:46 ] @
Radi pa ako zapne kazi gde je zapelo.
Postoji dosta slicnih integrala mozda si treba da probas prvo sa malo lakism primerima. [ dukowski @ 03.10.2011. 14:58 ] @
Problem je u tome sto se ovaj integral ne moze svrstati ni u jedan tip integrala sa polinomima, a ova smjena ne vodi nicemu...samo se dalje zapetljavas kad je stavis...
[ Nedeljko @ 03.10.2011. 15:00 ] @
I šta kaže Uščumlić, šta je rešenje?
[ pexxi92 @ 03.10.2011. 15:02 ] @
Neznam stvarno na koje tipove mislis ali ovom smenom se ovaj integral najlakse resava
Evo ti jos jedan "hint" nemoj odma da je primenis vec prvo malo transformisi gornju funkciju P.S. Neznam zasto si se uhvatio odma za taj integral, kao sto rekoh radi postepeno prvo lakse primere i resenje ce ti kasnije biti daleko jasnije [ dukowski @ 03.10.2011. 15:05 ] @
Nemam ga sad kod sebe pa ne znam napamet, ali koliko se sjecam imaju zbir ln i arctg sa nekim koeficijentima ispred, pod ln je bio malo duzi izraz, a pod arctg neki korijen kolicnika...tako otprilike izgleda koliko se sjecam...
[ Nedeljko @ 03.10.2011. 15:52 ] @
pexxi92
Ne zezaj čoveka sa takvim "hintovima". Ako znaš da rešiš zadatak reši ga. Ovo je samo zavlačenje u puvanje kako ti znaš, ali on neka malo provežba lakše primere. [ pexxi92 @ 03.10.2011. 16:43 ] @
Nedeljko podseticu te na pravila foruma
Ne ocekujte da neko uradi zadatak umesto vas vec probajte sami. Dakle ja sam mu rekao koju smenu da primeni i takodje rekao da prvo malo transformise izraz i koliko sam video on nije to probao pa zastao na nekom koraku. Takodje iz resenja je ocigledno da treba da se svede na racinalnu funkciju sto se gornjom smenom upravo postize. Ukoliko smatras da nisam upravu slobodno mu napisi resenje... [ dukowski @ 03.10.2011. 16:51 ] @
Ne trazim da se uradi zadatak, vec prvih nekoliko koraka...ako zaista ta smjena pomaze da se rijesi integral, sta da radim sa onim minusom dole uz ovakvu smjenu i kako da transformisem gornju funkciju da bih krenuo ka necemu cemu se nazire kraj...ovako, uz ovu smjenu i gomilu drugih koje sam probao, samo se vrtim u krug...radim ga od sinoc skoro bez prekida :)
Dakle, ako koristim smjenu koju si naveo, kako da transformisem gornju funkciju pod korijenom i kako da se oslobodim minusa u nazivniku? [ Nedeljko @ 03.10.2011. 19:11 ] @
Upravo tako. Pogledao sam predloženu smenu i ne vodi rešenju. Što se "hinta" koji glasi "prvo transformisati izraz" tiče, izraz bi se mogao analognom transformacijom transformisati i nakon smene i dobiti isti rezultat. Svejedno je da li se transformacije vrše pre ili posle smene.
Očigledno se radi o još jednom baronisanju člana pexxi92. [ Nedeljko @ 03.10.2011. 21:04 ] @
Evo, ja priznajem da sam pokušao da rešim ovaj integral i da nisam uspeo. Ko zna da ga reši, ima savršenu priliku da mi održi čas iz integrala. Znam da pojedincima to znači više nego leba da jedu.
P.S. Pojedinac je upravo obavešten preko privatne poruke. [ igorpet @ 03.10.2011. 21:45 ] @
Da li ste razmisljali u ovom pravcu? 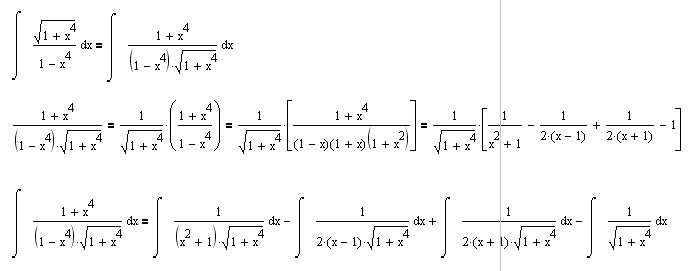 [ pexxi92 @ 03.10.2011. 22:23 ] @
Navikao sam na ovakvo ponasanje Nedeljka nije me ni briga.
Ja sam samo hteo da pomognem decku da nesto nauci a ne da mu odma dam celokupno resenje... [ Nedeljko @ 03.10.2011. 22:44 ] @
A ja sam navikao na tvoje baronisanje.
Rešenje ne znaš. Naravno da se onom smenom ne dobija integral racionalne funkcije. [ pexxi92 @ 03.10.2011. 22:47 ] @
Nedeljko
ako neznas kako da pomognes ne znam zasto se javljas na temu... Dukowski ako zelis napisacu detaljniji postupak. [ Nedeljko @ 03.10.2011. 22:57 ] @
Jedva čekam da vidim taj detaljniji postupak.
[ igorpet @ 03.10.2011. 23:04 ] @
Mozda je ovako bolje u odnosu na moj prvi predlog:
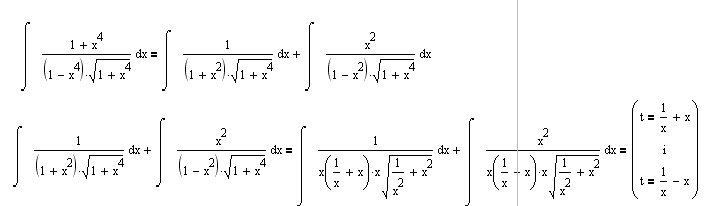 [ pexxi92 @ 03.10.2011. 23:05 ] @
Igore
Ok je ovo, smena x+1/x ili x-1/x takodje resava integral mada x^2+1/x^2 to radi brze i jednostavnije. Upravo smene tog tipa se koriste kod ovakvih integrala i to sam imao na umu kada sam rekao da treba prvo da proba sa laksim zadacima a ne da bi se "baronisao"... [ miki069 @ 03.10.2011. 23:14 ] @
X^2 = tg(t) vodi ka izlazu iz tunela.
Posle ove druge smene ostaje integral rastavljive racionalne funkcije, čime je rešen. [ Nedeljko @ 03.10.2011. 23:37 ] @
Bravo Miki genije!
Proverio sam tvoju smenu i zaista radi! Stvarno nisam znao ovo da rešim, a pokušavao sam. Svaka čast! [ dukowski @ 03.10.2011. 23:49 ] @
Sto je najgore, danas sam za neki drugi integral koristio smjenu x=tgt i ne sjetih se da probam sa x^2 u ovom...
Zahvaljujem se i svaka cast na ovako elegantnom postupku...hvala svim ljudima dobre volje :) [ miki069 @ 03.10.2011. 23:52 ] @
Ajd do kraja.
I kraju sam dobio isti đavo kao što su Pexxi92 i Igor sugerisali. Samo mi nije jasno kako bi ta smena funkcionisala od početka do kraja zadatka. Smena: x^2+1/x^2 = t mi nije funkcionisala. Milsim da treba: x^2+1/x^2 = 1/t^2 ili x^2+1/x^2 = t^2, a ne x^2+1/x^2 = t. [Ovu poruku je menjao miki069 dana 04.10.2011. u 07:52 GMT+1] [ pexxi92 @ 04.10.2011. 00:05 ] @
[ Nedeljko @ 04.10.2011. 06:24 ] @
[ pexxi92 @ 04.10.2011. 11:47 ] @
Nedeljko
Izvinjenje prihvaceno. Slazem se za apsolutnu vrednost naravno, bolje je podeliti razlomak sa x i onda do takvog problema ne dolazi. Ipak Nedeljo druze stari nakon 7 godina pocinjes da se menjas. Priznajem, odusevljen sam. [ Sonec @ 04.10.2011. 12:00 ] @
Citat: pexxi92: Nedeljko Ipak Nedeljo druze stari nakon 7 godina pocinjes da se menjas. Priznajem, odusevljen sam. Da, da, ovako si isto pisao i na onoj temi gde si govorio da imas naucne radove, a na nekim drugim temama nisi znao neke osnovne stvari i rekao si da imas 19 godina, sto znaci da.... ma zaboravi, hranim trola bezveze [ Nedeljko @ 04.10.2011. 12:23 ] @
Tih starih poruka se sećam, ali treba svakome priznati kad uradi nešto dobro. Ne vidim šta je tu sporno.
[ pexxi92 @ 04.10.2011. 12:32 ] @
Sonec
Niko se naucen nije rodio. Nisam znao, naucio sam, sad znam. Ili i ti spadas u grupu bogom danih "naucnika"? [ kandorus @ 04.10.2011. 16:37 ] @
Citat: Pod "pojedincem" sam inače mislio n kandorusa. Kad se "pojedinac" logovao na ES i primetio poruku pomislio je na smenu X^2 = tg(t). Medjutim problem je u to vreme već bio rešen. Pretpostavljam da je Nedeljko pokušao iz Mathematica http://www.wolframalpha.com/input/?i=Integrate[Sqrt[1%2Bx^4]%2F(1-x^4)%2Cx]&asynchronous=false&equal=Submit da reši integral i dobio je rešenje koje je sadržavalo AppellF1 funkciju. Verovatno je zato drugima osporavao rešenje. Zanimljiv integralčić. [ Nedeljko @ 04.10.2011. 16:59 ] @
Pojedinac može da troluje, jer je dokazao da ni polinom ne ume da integrali.
[ kandorus @ 04.10.2011. 18:35 ] @
Dakle, ipak te je Mathematica zavela ! Inače bi reagova na tu primedbu a ne bi dangubio sa trolovanjem.
[ Nedeljko @ 04.10.2011. 19:28 ] @
Ja matematiku nemam, a ko troluje, to posetioci mogu da procene.
[ Bojan Basic @ 04.10.2011. 19:30 ] @
Zadatak je rešen, nema smisla dalje nastavljati ovako kako je krenulo.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|