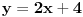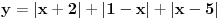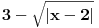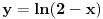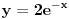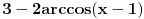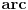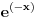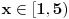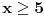[ patkan1992 @ 11.10.2011. 11:29 ] @
|
[ edisnp @ 11.10.2011. 12:37 ] @
za ovu prvu funkciju posto imas ove apsolutne vrijednosti najbrze ti je da koristis one tablice i odma vidis u kojim intervalima ti je fukncija definisana i sa kojim su predznacima ove apsolutne vrijednosti.
,evo kroz primjer cu ti objasniti 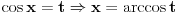 ,znaci da bih icsupao to x iz cosinusa moras da delujes inverznom funkcijom ,a inverzna funkcija od cosinusa je arccos ,znaci da bih icsupao to x iz cosinusa moras da delujes inverznom funkcijom ,a inverzna funkcija od cosinusa je arccos[ patkan1992 @ 11.10.2011. 14:38 ] @
Koje su to tablice? (posto nisam ni malo upucen u ovo.)
Moze neko da pomogne i oko ovih drugih funkcija? [ SrdjanR271 @ 11.10.2011. 15:20 ] @
[ SrdjanR271 @ 11.10.2011. 18:36 ] @
[ patkan1992 @ 13.10.2011. 09:24 ] @
@SrdjanR271, ne znam kako da nacrtam nijednu od tih.. Problem mi je oko ovih funkcija :/ Nisam pratio nastavu u srednjoj, sada mi se vraca... Ne razumem nista oko ovih primera koje sam naveo u prvom postu :(
[ Sonec @ 13.10.2011. 09:45 ] @
PATKAN
Nzm dal ste spominjali Tejlorov razvoj (verovatno niste), preko njega se kod nekih funkcija moze dosta lakse ispitati kosa asimptota i videti njeno ponasanje.... Ne svidja mi se samo kako su stavili da se nalazi  kod kose asimptote, ja bih stavio kod kose asimptote, ja bih stavio 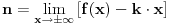 (ovde imas dva limesa), tj. stavio bih sa zagradom. (ovde imas dva limesa), tj. stavio bih sa zagradom.[Ovu poruku je menjao Sonec dana 13.10.2011. u 10:59 GMT+1] [ patkan1992 @ 14.10.2011. 22:54 ] @
@Sonec,
Bukvalno, ali bukvalno ovo sto citam nista ne razumem, kao da se traka zamrsila. Cujem, a ne razumem nista. :( Mozes li da mi objasnis na onim primerima odozgo? Mislim da cu tako najbolje razumeti kako se radi... Sledece nedelje vec imam neki test na fakultetu, i to bas ovo... Znaci imam nekih 5 dana da se snadjem da naucim da crtam funkcije. :( Nadam se da ces mi ti ili neko drugi pomoci oko ovoga. I hvala puno unapred! [ Sonec @ 14.10.2011. 23:00 ] @
A jesi li pokusao da shvatis resene primere koji su dati?
[ patkan1992 @ 14.10.2011. 23:59 ] @
Mislis na ovo sto je Srdjan nacrtao? (Ako na to mislis, ja ne kapiram za koji je to primer resenje). Treba mi pocetak, tj. objasnjenje kako se pocinje rad ovakvih zadataka. Tj. kako da zapocnem da nadjem te koordinate... Nista ne razumem... Bas bas ne znam ovo da radim. Nista mi nije jasno. Kao da je nesto potpuno novo za mene. :(
[ Sonec @ 15.10.2011. 00:03 ] @
4.
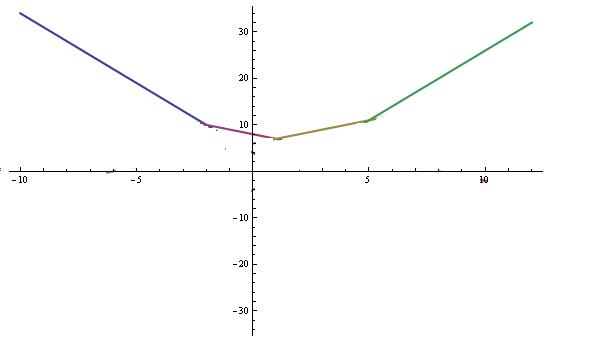
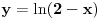 1. Trazimo domen date funkcije, odnosno vrednosti koje  moze da uzima. Logaritamska funkcija moze da uzima. Logaritamska funkcija 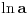 je definisana kada je je definisana kada je  , pa shodno tome, nasa posmatrana funkcija je definisana za , pa shodno tome, nasa posmatrana funkcija je definisana za 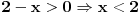 , tj. , tj. 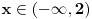 2. Nula funkcije je  . Odredjujemo znak funkcije, kada je pozitivna ( . Odredjujemo znak funkcije, kada je pozitivna (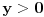 ) i kada je negativna ( ) i kada je negativna ( ), pri cemu pazimo da ), pri cemu pazimo da  moze da uzima samo vrednosti iz DOMENA!!! Pa odatle sledi da je moze da uzima samo vrednosti iz DOMENA!!! Pa odatle sledi da je  za za 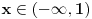 (sto pripada domenu) i (sto pripada domenu) i 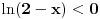 za za 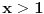 , al s obzirom da , al s obzirom da  mora pripadati domenu, onda je funkcija negativna za mora pripadati domenu, onda je funkcija negativna za 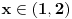 3. Funkcija nije ni parna ni neparna, to je lako da se proveri. 4. Asimptote: 1) horizontalna asimptota  pa ona ne postoji (nismo gledali slucaj pa ona ne postoji (nismo gledali slucaj 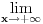 jer jer  ne moze da tezi ka ne moze da tezi ka 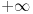 (zbog domena)) (zbog domena))2) vertikalna (gledas u granicnim tackama, ovde je to 2, i to limes sa leve strane) 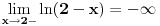 , pa je prava , pa je prava 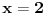 vertikalna asimptota, i vertikalna asimptota, i  se priblizava njoj sa leve strane u minus beskonacnosti. se priblizava njoj sa leve strane u minus beskonacnosti.3)kosa asimptota je prava oblika 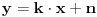 gde se gde se 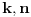 dobijaju iz uslova: dobijaju iz uslova: 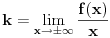 , a za , a za  sam ti vec napisao u mom 1 postu. Aj sad da to primenimo na nas zadatak: sam ti vec napisao u mom 1 postu. Aj sad da to primenimo na nas zadatak: 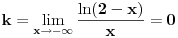 (limes se moze resiti preko lopitala lako, a (limes se moze resiti preko lopitala lako, a  tezi samo ka tezi samo ka 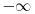 zbog domena (pisao sam to vec za horizontalnu)). S obzirom da je zbog domena (pisao sam to vec za horizontalnu)). S obzirom da je 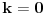 , to je nasa kosa asimptota u stvari horizontalna ( , to je nasa kosa asimptota u stvari horizontalna ( ), a ona ne postoji (sto smo vec pokazali), tako da ne postoji ni kosa. ), a ona ne postoji (sto smo vec pokazali), tako da ne postoji ni kosa.5. Monotonost, nadjes 1 izvod, i dobijas da za 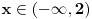 nasa data funkcija opada nasa data funkcija opada6. Konveksnost, drugi izvod (1 izvod na 1 izvodu (koji si vec nasao)), i dobijas da nasa funkcija je konkavna na domenu 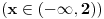 I na kraju ti ostaje da nacrtas grafik GRAFIK, grafik treba da bude samo realan deo na 2 slici [Ovu poruku je menjao Sonec dana 15.10.2011. u 01:54 GMT+1] [ Sonec @ 15.10.2011. 00:16 ] @
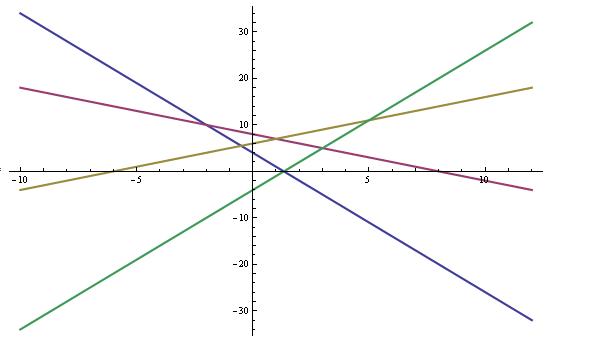
Srdjanovo resenje se dobija resavanjem apsolutnih vrednosti i crtanjem odgovorajucih pravih, u zavisnosti od domena. To je resenje za prvi primer.
Pa pogledaj link koji sam ti poslao, tu imas DETALJNO objasnjeno ispitivanje na primerima. [ Sonec @ 15.10.2011. 00:45 ] @
3.
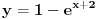 1.Domen 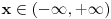 2. Nula funkcije 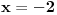 . Funkcija je pozitivna za . Funkcija je pozitivna za 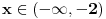 , a negativna za , a negativna za 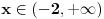 3. Nije ni parna ni neparna 4. Asimptote 1) horizontalna,  nije horizontalna kad nije horizontalna kad 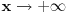 , ali , ali 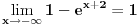 , pa je , pa je 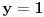 horizontalna za horizontalna za 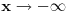 2) vertikalna, nema, jer je domen ceo skup R 3) kose nema kad 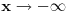 jer tada postoji horizontalna, a jer tada postoji horizontalna, a 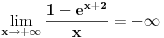 , pa ne postoji kosa za , pa ne postoji kosa za 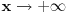 5. monotonost, f-ja je opadajuca, na celom domenu 6. konveksnost, f-ja je konkavna, na celom domenu GRAFIK FUNKCIJE: www.wolframalpha.com/input/?i=1-e^%28x%2B2%29 Sad uradi sam 5. primer [ Sonec @ 15.10.2011. 10:22 ] @
[ patkan1992 @ 15.10.2011. 13:25 ] @
To je problem, gubili smo 6 casova vezbi a imali predavanja.. Rekla nam je da uradimo kako znamo domaci.. Ali u cetvrtak nam svakako daje test.. Funkcije i Kompleksne brojeve...
Vracam se danas za Bg, pa cu pogledati sve ovo sto si mi dao. Ako se ne snadjem, javicu sta mi nije jasno. :) Hvala veliko! Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|