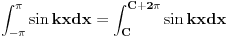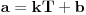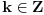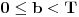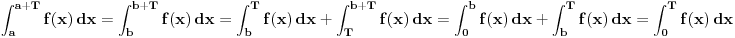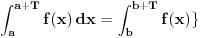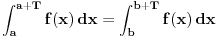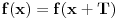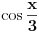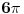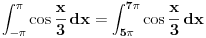Neka je funkcija sa periodom i neka je za i

.

Zasto je to tako? Ima neki prost dokaz?

Koji korak nije jasan?

Ovaj

Prema postavci, intervali [a,a+T] i [b,b+T] se razlikuju za kT pa T-periodicna funkcija f uzima iste vrednosti na njima.

Ovo važi



Ako je funkcija periodična.Inačne ne.Dakle samo ako je



Nacrtaj neku od takvih funkcija i šrafiraj površinu koja predstavlja određeni integral sa granicama razmaka "T",bilo gdje na x osi.

Ovde treba razmotriti vrednosti k. Za , nije period.

Za -periodičnu funkciju važi za sve i .

Ne ide mi sa Latexom, baš sam se trudila. Elem, probaj sa integralom cos(x/3) u granicama od -pi do pi, i u ganicama od 0 do 2 pi.
Je li moguće da grešim na elementarnim integralima?

@kacuncica

Period funkcije je , tako da je integral

Aha. Razumela sam da @matematikuvolim misli da može da uzme bilo koje C, tj. bilo koje granice na rastojanju 2 pi.