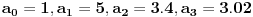
Znas kako, budes malo kvaran, i pretpostavis da je niz konvergentan (ogranicen i monoton), i pustis limes, i dobijes da je limes 3 ili -3. Cini se da je resenje 3 verovatnije, al nista nije sigurno. Ajde da pretpostavimo da je resenje 3. Imamo 2 opcije, niz je opadjuci i ogranicen odozdo, il, niz je rastuci i ogranicen odozgo. Sta cemo sad, pa proverimo prvih nekoliko clanova, i sta dobijamo: . 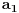Primecujemo, da nas niz, od nekog clana, tacnije od , da opada, i da clanovi niza, kako raste, postaju sve blize i blize trojci. Kako nas niz opada (to cu kasnije pokazati, al primecuje se), da bi konvergirao, on mora da je ogranicen odozdo. I to sa trojkom. 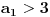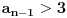Tu cinjenicu dokazujemo matematickom indukcijom: , pretpostavimo , i dokazujemo da je .
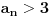
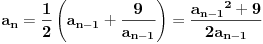
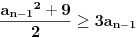
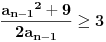
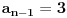
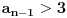
Pa, . Primenimo nejednakost izmedju aritmeticke i geometrijske sredine i dobijamo , tj. , a jednakost vazi samo za , ali po induktivnoj pretpostavci je , pa je .
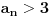
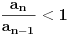
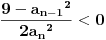
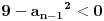
Treba da pokazemo jos i da je niz monotono opadajuci, tj. , sto se svodi na , tj. , a to je tacno jer je .

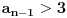
I to je to, imas da je niz od nekog clana ogranicen odozdo i opadajuci, to znaci da konvergentan.

Granicnu vrednost ces lako naci vec sam....

Hvala!!