[ varpix.bh @ 09.11.2011. 09:46 ] @
| Koliko ima racionalnih clanova u razvju binoma? Buni me ovo 1266 jer se ne moze skratiti sa 5 kada se binom razvije.... Ako moze pomoc od nekog ? Unaprijed, hvala :) (5^sqr(3) + 7^sqr(2))^1266 |
|
[ varpix.bh @ 09.11.2011. 09:46 ] @
[ Sonec @ 09.11.2011. 10:39 ] @
Clanovi binomnog obrasca (za
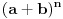 )se odredjuju prema formuli: )se odredjuju prema formuli: 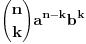 , gde je , gde je 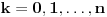 E sad, ovaj binomni koeficijenat 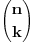 nam sad nije bitan, on nam nece uticati na resenje. nam sad nije bitan, on nam nece uticati na resenje.Tvoji clanovi ce biti oblika 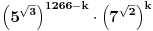 . Tebi ovde problem prave . Tebi ovde problem prave 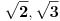 , a kada ce koreni nestati, pa onda kada , a kada ce koreni nestati, pa onda kada 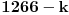 i i  jesu parni. I onda na kraju zakljucujemo da je resenje jesu parni. I onda na kraju zakljucujemo da je resenje 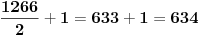 Moguce je da sam pogresio, al ne mogu sad da gledam, zurim na faks. [ varpix.bh @ 09.11.2011. 14:22 ] @
ne znam kako pisati ove formule ovdje na forumu ali u mom slucaju je "peti korijen od tri i sedmi korijen od 2 u zagradi pa sve na 1266... Sad je problem sto kad se rijesim korijena dobijam 3 na 1/5 pa sve na 1266-k sto mnozi 2 na 1/7 pa sve na k (tj. kad se razvije po ovoj formuli gore)... bilo bi puno lakse za objasniti da znam kako upisati formule na forumu...
[ djoka_l @ 09.11.2011. 14:42 ] @
[ darkosos @ 09.11.2011. 14:58 ] @
O boze :) Da, bilo bi puno lakse... http://www.elitesecurity.org/t35291-Sve-La-TeX-na-ovom-forumu
A i kad kliknes na slicicu tex formule, izaci ce ti kako je napisano originalno... Znaci 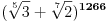 ? Pa to je onda kao sto je Sonec napisao, samo imas da su ti celi brojevi ? Pa to je onda kao sto je Sonec napisao, samo imas da su ti celi brojevi 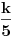 i i 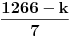 Posto 1266 nije deljivo ni sa 5 ni sa 7, k mora biti deljivo sa oba. Dakle, odgovor je koliko ima brojeva deljivih sa 35 u skupu {1,..,1266} (0 ne moze). A to bi trebalo da je ceo deo od 1266/35, a to je 36. [ varpix.bh @ 09.11.2011. 15:20 ] @
[ varpix.bh @ 09.11.2011. 19:27 ] @
I sta sad ?
[ darkosos @ 09.11.2011. 19:55 ] @
I ja sam malo prolupao...
Ajde uzecu kako si ti napisao, dakle 1266-k treba da je daljivo sa 5 a k sa 7. Posto 1266 = 253*5+1, onda to znaci da k treba da je oblika m*5+1. Brojeva ovog oblika izmedju 1 i 1266 su 1, 6, 11, ..., 1266. Treba naci one koji su deljivi sa 7. [ SrdjanR271 @ 09.11.2011. 20:39 ] @
[ edisnp @ 09.11.2011. 20:43 ] @
Evo neke ideje
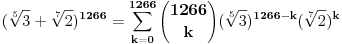 i sad ocigledno slijedi da mora da bude i sad ocigledno slijedi da mora da bude 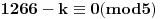 i istovremeno i istovremeno 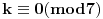 tj. tj. 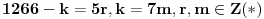 i onda je minimalno i onda je minimalno  koje zadovoljava relaciju jedanko 3 tj. vrijednost jednog takvog k je koje zadovoljava relaciju jedanko 3 tj. vrijednost jednog takvog k je 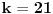 pa se problem svodi na to da u polinomu pa se problem svodi na to da u polinomu 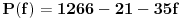 nadjemo maksimalno nadjemo maksimalno  takvo da je takvo da je 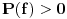 maksimalno maksimalno 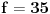 pa za relacije pa za relacije 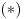 slijedi da takvih slijedi da takvih  ima ima 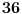 pa bi valjda trebalo da racinalnih clanova ima pa bi valjda trebalo da racinalnih clanova ima 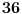 [ SrdjanR271 @ 09.11.2011. 21:02 ] @
Ako je to pitanje, 36 je tačan odgovor.
[ varpix.bh @ 09.11.2011. 21:07 ] @
Citat: SrdjanR271: Ja bih pomogao ali nisam siguran šta je tačno zadatak? Koliko ima racionalnih clanova u razvju binoma 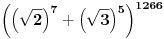 ili ili 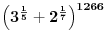 ? ?Taj drugi 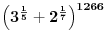 [ edisnp @ 09.11.2011. 21:15 ] @
Pa dobio si rjesenje.
[ varpix.bh @ 09.11.2011. 21:21 ] @
Hvala :)
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|