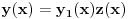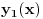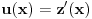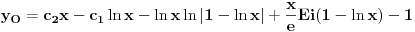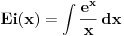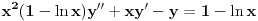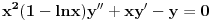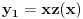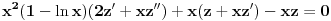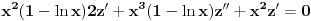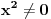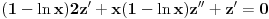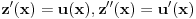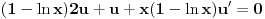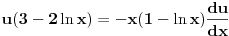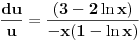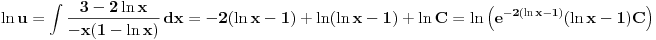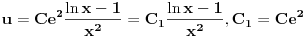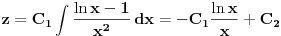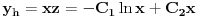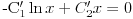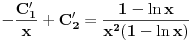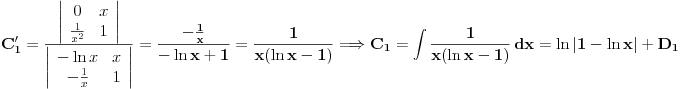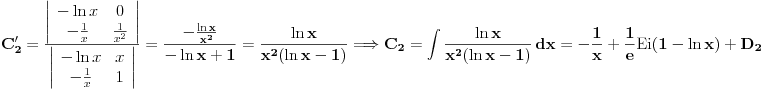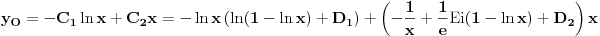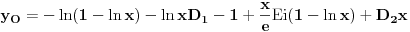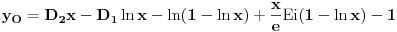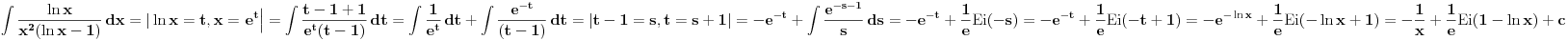Zadatak iz diferencijalne jednačine

[ Nikola 23 @ 09.11.2011. 12:12 ] @

Zadatak glasi: Naći opšte rešenje diferencijalne jednačine: x^2*(1-lnx)*y''+x*y'-y=(1-lnx), ako je poznato jedno rešenje homogene y1=x.

Kako se ovo rešava? Da li je isto kao kada bi s desne strane od jednako bila 0, ili ne? Je'l zna neko šablon?
Hvala!:-)

[ Nedeljko @ 09.11.2011. 16:17 ] @

Prvo reši homogenu jednačinu. Njoj ćeš sniziti red za jedan uvođenjem najpre smene

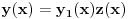
, gde je

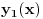
jedno poznato rešenje homogene jednačine. Dobićeš homogenu jednačinu u kojoj se ne pojavljuje nediferencirana nepoznata funkcija, pa onda uvedi smenu

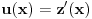
. Time ćeš sniziti red jednačine za jedan. Zapamti dobro ovaj opšti postupak snižavanja reda homogene linearne diferencijalne jednačine kada je poznato bar jedno netrivijalno rešenje! Onda imaš linearnu homogenu jednačinu prvog reda, koja je rešava na uobičajen način. Tako ćeš rešiti homogenu jednačinu. Onda možeš rešiti nehomogenu Lagranževom metodom varijacije proizvoljnih konstanti.

[ SrdjanR271 @ 09.11.2011. 20:25 ] @

Opšte rešenje je:

, gde je

Ako ne uspeš da rešiš javi ovde, ja sam uradio ceo zadatak, al me mrzi da kucam ceo.

_{[Ovu poruku je menjao SrdjanR271 dana 10.11.2011. u 02:00 GMT+1]}

[ SrdjanR271 @ 10.11.2011. 01:19 ] @

Ajde da napišem rešenje, možda nekome bude od koristi.