[ real one @ 10.11.2011. 18:40 ] @
| odrediti karaktaristicne vrijednosti matrice A= 0 1 1 -1 1 0 -1 1 1 -1 0 1 -1 1 1 0 a zatim koristeci Hornevu shemu ispitati da li je Z0=-1 nule karaktaristicnog polinoma |
|
[ real one @ 10.11.2011. 18:40 ] @
[ SrdjanR271 @ 10.11.2011. 18:43 ] @
Lep zadatak.
[ miki069 @ 11.11.2011. 02:21 ] @
Jel znaš šta je karakteristična matrica date matrice A?
Jel znaš šta je karakteristični polinom? Jel znaš šta su karakteristične vrednosti? Što reče Srđan baš "lep zadatak". Može i da se produži (ako je tačno ovo pod c): c) Ispitati da li matrica A dopušta dijagonalizaciju? d) Naći njoj sličnu dijagonalnu matricu B. e) Naći matricu prelaska P, takvu da važi A*P = P*B. f) Za svaku karakterističnu vrednost odrediti karakteristične vektore, bazu i dimeziju vektorskog prostora. g) Naći minimalni polinom matrice A. h) Izračunati matricu A^n i) Dokazati matematičkom indukcijom trvđenje pod h) Standardan zadatak sa ispita iz predmeta "Linerana algebra i polinomi" na PMF-u. Rešenje je na oko 17 sitno pisanih stranica, A4 formata. Ko ga uradi bez greške automatski je oslobođen usmenog dela ispita. [ SrdjanR271 @ 11.11.2011. 02:23 ] @
[ real one @ 11.11.2011. 10:25 ] @
hvala puno Srdjane
[ real one @ 11.11.2011. 22:17 ] @
al kako ovo (-3,1,1,1)???
[ Sonec @ 11.11.2011. 22:35 ] @
Sopstvene vrednosti predstavljaju nule karakteristicnog polinoma, a to su u ovom primeru -3 i 1.
[ real one @ 11.11.2011. 22:37 ] @
Da,skontao sam to,al odakle ono ostalo (1,1)??
[ Sonec @ 11.11.2011. 22:42 ] @
[ real one @ 11.11.2011. 22:45 ] @
pa jeste konfuzno jer je Srdjan na kraju napiso tr(A)=-3+1+1+1=0. zato mi je bilo cudno a Hvala ti
[ Sonec @ 11.11.2011. 23:10 ] @
[ SrdjanR271 @ 12.11.2011. 01:11 ] @
Citat: real one: al kako ovo (-3,1,1,1)??? 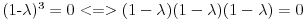 zato je 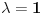 tri puta. 1 je nula karakterističnog polinoma višestrukosti tri. tri puta. 1 je nula karakterističnog polinoma višestrukosti tri.[ SrdjanR271 @ 12.11.2011. 01:17 ] @
Citat: Sonec: E sad, da li mora biti ispunjeno da je zbir nula karakteristicnog polinoma jednak tragu (ovo zakljucujem iz Srdjanovog posta), ja ne znam. Uvek. (Mora) Trag je uvek jednak sumi svojstvenih vrednosti. Da nisam računao višestrukost ne bih dobio nula. http://en.wikipedia.org/wiki/Trace_(linear_algebra) [ Nedeljko @ 12.11.2011. 09:07 ] @
Suma svojstvenih vrednosti jednaka je tragu matrice, a proizvod determinanti. To lako sledi iz Vijetovih formula i definicije karakterističnog polinoma.
[ Sonec @ 12.11.2011. 09:27 ] @
[ djolas ba @ 08.01.2012. 00:22 ] @
3.[5+5] a) Odrediti sve nule kompleksnog polinoma P(u indexu 5) = ix^5 +1
b) Neka je K skup svih nula polinoma P5(x). Ispitati koje osobine posjeduje al- gebarska struktura (K,*), gdje je * mnozenje kompleksnih brojeva. Moze pomoc? Hvala unaprijed! Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|