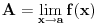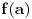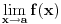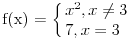[ 4co_R @ 11.11.2011. 16:54 ] @
|
[ Sonec @ 11.11.2011. 17:42 ] @
Definicija 1. Neka je
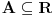 . Tacka . Tacka  je tacka nagomilavanja skupa je tacka nagomilavanja skupa  ako za ako za 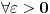 je je 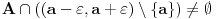 . . I to oznacavamo sa 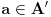 Definicija 2. Neka je 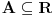 , , 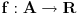 i i 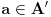 . Tada kazemo da je . Tada kazemo da je 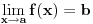 ako vazi ako vazi 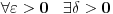 tako da za tako da za 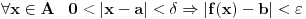 Limes funkcije nikada ne zavisi od toga kolika je vrednost funkcije u tacki  (za izracunavanje granicne vrednosti). (za izracunavanje granicne vrednosti).Aj da malo rastavimo ovaj izraz 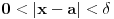 , to znaci da , to znaci da 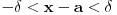 i i 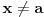 , tj. , tj. 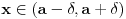 i i 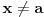 . .[ 4co_R @ 11.11.2011. 19:04 ] @
Ali ako je funkcija def u tacki nagomilavanja onda limes dobijam tako sto svugde umesto x zamenim vrednost kojoj on tezi tj limf(x)=f(a)...
p.s. Ne umem dobro da objasnim sta me buni :)) [ Sonec @ 11.11.2011. 19:31 ] @
Evo, morao sam da otvorim Analizu 1 od Kadelburga da pogledam kako su tamo rekli. Tamo se nalazi slicna definicija (preko okolina, al oznacava isto) i pise zatim sledece:
Citat: Granicna vrednost funkcije u nekoj tacki se definise i svaka dalja polemika je nepotrebna. [ Nedeljko @ 11.11.2011. 20:28 ] @
Citat: 4co_R: Ali ako je funkcija def u tacki nagomilavanja onda limes dobijam tako sto svugde umesto x zamenim vrednost kojoj on tezi tj limf(x)=f(a)... p.s. Ne umem dobro da objasnim sta me buni :)) To radiš kada je funkcija definisana i neprekidna u toj tački. Sve elementarne funkcije su neprekidne, tako da to što si napisao možeš raditi sa elementarnim funkcijama. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|