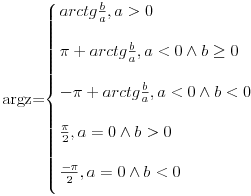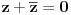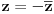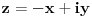Ako posmatras z = a+ib kao tacku (a,b) u pravouglom koordinatnom sistemu, a=0 znaci da se tacka nalazi na y-osi.
I onda imas dve mogucnosti: nalazi se iznad x-ose, tj b>0, i onda je ugao pi/2; obrnuto, ako je b<0 onda je ispod x-ose i ugao je -pi/2.
Nemam volje da crtam :)

To sam vec razumeo nego kada je u drugom kvadrantu mislim da je ovo pi+acrtg(b/a) ustvari pi-(-arctg(b/a)),a za 3. kvadrant meni bi bilo logicno da je argZ=pi+acrtg(b/a) medjutim nije O.o

pi+acrtg(b/a) i -pi+acrtg(b/a) su isti uglovi :) jer se razlikuju za 2pi. Verovatno je stvar dogovora, jer to zavisi od toga da li zelimo da je argz u intervalu -pi,pi ili 0,2pi

Da ne otvaram novu temu, isto se tice kompleksnih brojeva. Treba mi graficka interpretacija ovoga.

Resio sam ga ovako ali ne znam da nacrtam posto su opsti brojevi

Z i su osno simetricni u odnosu na realnu osu.Ako je njihov zbir jednak nula realni delovi su im 0.