Nema opšte fore preko kvadratura, ali za , gde su i polinomi, a i konstante postoji fora. Dakle, kada je tog oblika, onda nije problem.

Lagranžov metod varijacije konstanti.

Jao, da, gde njega smetnuh s uma.

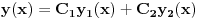
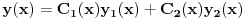
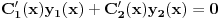
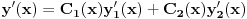
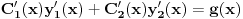
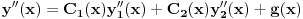
Dakle, ako je opšte rešenje homogene jednačine , partikularno ćemo potražiti u obliku . Ako je pritom , onda je . Ako je pritom , onda je i samim tim .

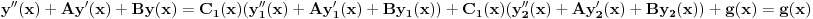
Dakle, treba rešiti sistem jednačina

,
.

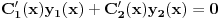
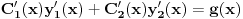
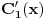
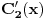
Prvo reši ovaj sistem po i kao sistem linearnih jednačina, a onda izvrši integraciju. Ako ne nodbaciš integracione konstante, dobićeš opšte rešenje nehomogene jednačine, a ako ih odbaciš, dobićeš jedno partikularno rešenje.