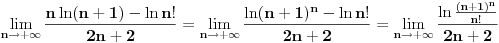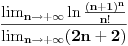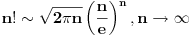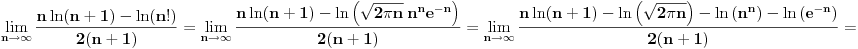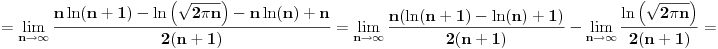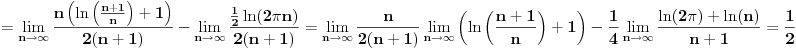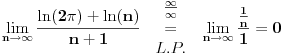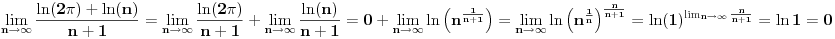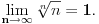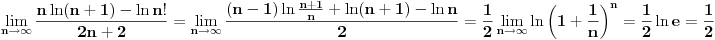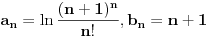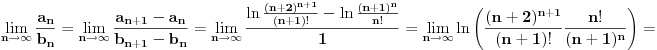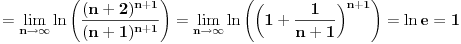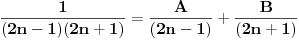[ pitomir @ 29.11.2011. 15:12 ] @
|
[ SrdjanR271 @ 29.11.2011. 15:22 ] @
Prvo što mi pada na pamet je Stirlingova formula.
[ pitomir @ 29.11.2011. 15:39 ] @
Uf, nisam cula za tu formulu. Ovo je zadatak sa jednog od proslogodisnjih kolokvijuma na pmf-u za prvu godinu.
[ SrdjanR271 @ 29.11.2011. 15:42 ] @
[ pitomir @ 29.11.2011. 16:09 ] @
[ pitomir @ 29.11.2011. 16:15 ] @
Hm, ne smem da koristim lopitalovo pravilo, nismo to jos radili (tj. secam se toga iz srednje skole, ali sumnjam da bi mi asistent priznao kad bih tako uradila na kolokvijumu).
[ SrdjanR271 @ 29.11.2011. 16:20 ] @
[ pitomir @ 29.11.2011. 16:30 ] @
Sad sam razumela. Ne, mislim da mi ne bi priznali ni kad bih koristila Strilingovu formulu, posto je nismo pominjali. Ali korisno je ovako znati, naravno. A radili smo asimptotske oznake tipa malo o, veliko O i tilda. Pokusavala sam sa malim o, ali me je bunilo sto n tezi ka beskonacno, pa ne mogu da primenim onih nekoliko formula, jer one vaze samo kad n tezi ka nuli. A takodje me bunio n!.
[ Nedeljko @ 29.11.2011. 16:47 ] @
[ Nedeljko @ 29.11.2011. 16:56 ] @
Drugo, kod Stirlingove formule treba biti oprezan. Ne sme se primenjivati kao da je
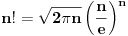 jer to nije tačno. Ne kažem da si je tako napisao, ali si je tako primenio. Zapravo, postoji niz jer to nije tačno. Ne kažem da si je tako napisao, ali si je tako primenio. Zapravo, postoji niz 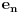 koji teži nuli takav da je koji teži nuli takav da je 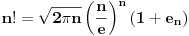 (zapravo je (zapravo je 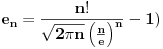 ), te je ), te je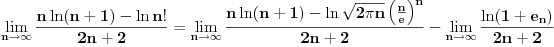 itd. itd.odakle će se videti kako nam 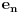 u limesu otpada. Bez toga rešenje sa Stirlingovom formulom nije kompletno. u limesu otpada. Bez toga rešenje sa Stirlingovom formulom nije kompletno.[ SrdjanR271 @ 29.11.2011. 17:06 ] @
[ pitomir @ 29.11.2011. 17:06 ] @
Da, tacno, moze preko Stolcove teoreme. Nisam se toga setila. Hvala puno obojici! :)
[ SrdjanR271 @ 29.11.2011. 17:12 ] @
Citat: Nedeljko: Drugo, kod Stirlingove formule treba biti oprezan. Ne sme se primenjivati kao da je 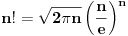 jer to nije tačno. Ne kažem da si je tako napisao, ali si je tako primenio. Zapravo, postoji niz jer to nije tačno. Ne kažem da si je tako napisao, ali si je tako primenio. Zapravo, postoji niz 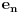 koji teži nuli takav da je koji teži nuli takav da je 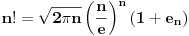 (zapravo je (zapravo je 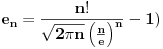 ), te je ), te je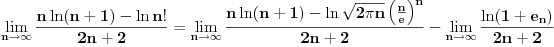 itd. itd.odakle će se videti kako nam 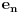 u limesu otpada. Bez toga rešenje sa Stirlingovom formulom nije kompletno. u limesu otpada. Bez toga rešenje sa Stirlingovom formulom nije kompletno.Slažem se u potpunosti. Hteo sam da napišem ovako 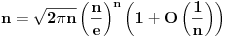 ali reko da ne zakomplikujem, da je ne zbunim. [ Sonec @ 29.11.2011. 18:41 ] @
Ako je u pitanju MATF u Beogradu, onda se Stirlingova formula uci u II semestru, u maju mesecu, kod redova.
[ pitomir @ 29.11.2011. 20:11 ] @
Jeste MATF. Hvala na informaciji :)
[ Sonec @ 29.11.2011. 20:49 ] @
Citat: pitomir: kako si izracunao 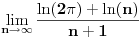 ? ?Vec si dobila odgovor na ovo pitanje, al moze i na drugi nacin. 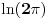 je neki broj, i to te ne zanima (jer imas oblik je neki broj, i to te ne zanima (jer imas oblik 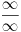 pa konstanta ne utice na limes), tako da pomatras samo ostatak i imas logaritamsku kroz stepenu funkciju, stepena brze tezi beskonacnosti pa je taj limes jednak nuli. pa konstanta ne utice na limes), tako da pomatras samo ostatak i imas logaritamsku kroz stepenu funkciju, stepena brze tezi beskonacnosti pa je taj limes jednak nuli.[ pitomir @ 29.11.2011. 21:41 ] @
E pa da, tacno, to je jos jednostavnije.
Imam jos jedno pitanje, ako neko zna. Kao sto ovaj niz: 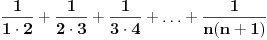 moze da se napise i ovako: 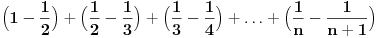 , da li po nekom slicnom sistemu moze da se napise niz , da li po nekom slicnom sistemu moze da se napise niz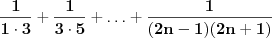 ? ?Pokusala sam ovako: 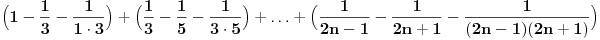 , ali tako sam samo zakomplikovala, posto treba da izracunam limes niza kad , ali tako sam samo zakomplikovala, posto treba da izracunam limes niza kad 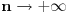 . .[Ovu poruku je menjao pitomir dana 29.11.2011. u 23:11 GMT+1] [Ovu poruku je menjao pitomir dana 29.11.2011. u 23:12 GMT+1] [ miki069 @ 30.11.2011. 00:51 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|