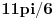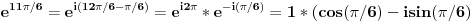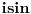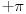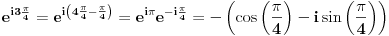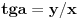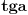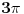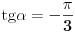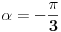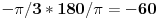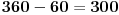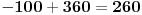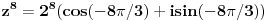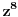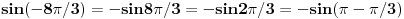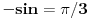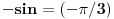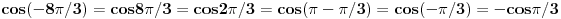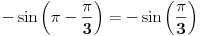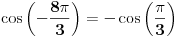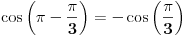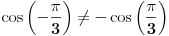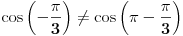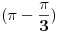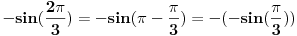|
|
[ patkan92 @ 02.12.2011. 11:32 ] @
|
| Pozdrav pre svega :)
Treba mi pomoc oko jednog zadatka sa matematiranja, rec je o trigonometrijskom obliku kompleksnog broja... Na slici sam uokvirio sta mi nije jasno, a to je kako se gubi ovo "minus" ispred  kod kosinusa i sinusa. Mozda su izvukli minus, ali ne razumem kako. :/ kod kosinusa i sinusa. Mozda su izvukli minus, ali ne razumem kako. :/
Evo slike:
http://i39.tinypic.com/adbuz8.png
I, ako bi neko mogao da mi objasni neku "caku" kako da gledam ove uglove kod ovakvih tipova zadataka. Ili moram onaj trigonometrijski krug da ucim napamet (to mi bas i nije po volji) :p
Hvala unapred! :) |
[ djoka_l @ 02.12.2011. 11:43 ] @
Kosinus je parna funkcija, a sinus je neparna funkcija. To znači da je cos(-x)=cos(x), a da je sin(-x)=-sin(x). Tako su "nestali" minusi.
Što se tiče ugla, nije mi jasno šta pitaš. U zadatku koji si dao kao primer, ugao se računa kao atan od imaginarnog dela podeljenog sa realnim delom. E sada ako su oba broja (i realni i imaginarni) pozitivni, znači da je ugao u prvom kvadrantu (između nula i pi pola), za imaginarni deo pozitivan a realni negativan drugi kvadrant, oba negativna treći kvadrant i imaginarni negativan a realni pozitivan četvrti kvadrant.
[ patkan92 @ 02.12.2011. 11:53 ] @
Hvala na ovom prvom, sad mi je jasno. :)
A sto se tice ovog drugog pitanja, na primer kada dobijem ugao  , kako da ja znam da je taj ugao jednak uglu 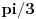 .
Ili ovde  , po kom pravilu se doslo do  ? I posle kako da znam koliko je i u kom je kvadrantu to  ? Valjda sam sada bio jasniji... [ djoka_l @ 02.12.2011. 12:05 ] @
Sinus i kosinus su periodične funkcije sa periodom od  .
To znači da je 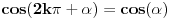 i da je  .
Ugao od 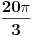 možeš da napišeš kao  .
[ Nedeljko @ 02.12.2011. 12:10 ] @
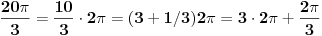 .
Koristi činjenicu da su trigonometrijske funkcije  -periodične. Dakle, 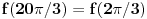 , gde je  bilo koja trigonometrijska funkcija.
Osim toga, ugao uvek možeš svesti na interval 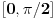 . Naime, osim što je sinus neparna a kosinus parna funkcija, pa ugao možeš svesti na opseg 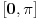 , važi još i  i 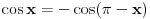 . [ patkan92 @ 02.12.2011. 16:55 ] @
Znam da moze tako da se napise, ali kako da znam posle taj ugao, na primer, od  koliko je? On je 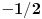 , to vidim iz zadatka, i minus je zato sto je kosinus u drugom kvadrantu negativan, ali kako da znam da je  isti ugao kao i 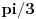 u prvom kvadrantu... Nadam se da je sada jasnije sta mi nije jasno..
I sta tacno znaci to da je periodicna 2kpi? Zasto se to 2kpi "gubi"? [ cikin @ 02.12.2011. 17:03 ] @
 jednostavno kad obrnes krug dodjes na istu vrednost!! [ patkan92 @ 02.12.2011. 17:14 ] @
Ok, to sam razumeo. Hvala!
A sto se tice ovoga?
Citat: Znam da moze tako da se napise, ali kako da znam posle taj ugao, na primer, od koliko je? On je , to vidim iz zadatka, i minus je zato sto je kosinus u drugom kvadrantu negativan, ali kako da znam da je isti ugao kao i u prvom kvadrantu... Nadam se da je sada jasnije sta mi nije jasno.. [ Sonec @ 02.12.2011. 17:18 ] @
To ti je Nedeljko vec odgovorio:
Citat: Nedeljko: Naime, osim što je sinus neparna a kosinus parna funkcija, pa ugao možeš svesti na opseg 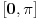 , važi još i  i 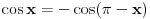 .
Ako je ugao  u prvom kvadrantu, onda ce ugao  biti u drugom (jer je  u prvom). [ patkan92 @ 02.12.2011. 17:22 ] @
Znaci bice: 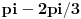 ? [ patkan92 @ 02.12.2011. 17:28 ] @
I je l isto vazi i za kada je taj neki ugao u trecem ili cetvrtom kvadrantu? Isto  ? [ Sonec @ 02.12.2011. 17:33 ] @
Ako mislis na vrednost 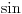 tih uglova, onda, da, bice isti.
Citat: patkan92: I je l isto vazi i za kada je taj neki ugao u trecem ili cetvrtom kvadrantu? Isto  ? 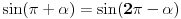 , gde je 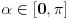 ako zelis da ostanes u trecem, odnosno cetvrtom kvadrantu. [ patkan92 @ 02.12.2011. 18:19 ] @
Sad tek nista ne razumem...
Koje formule vaze za sinus, a koje za kosinus? Meni treba znaci samo kako da gledam ove uglove kod trigonometrijskog oblika kompleksnog broja. Znaci kako da svodim na prvi kvadrat (ili kako se vec to zove), na one tablicne vrednosti uglova...
Kako da, na primer, sledece uglove svedem na tablicne vrednosti (prvi kvadrant)?


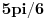
1. Kako da gledam u kom se oni kvadrantu uopste i nalaze?
2. Kako da ih svedem na poznate vrednosti (od 0 do 90 stepeni)?
3. Zanima me i za sinus i za kosinus, jer kod trigonometrijskog oblika kompleksnog broja, mi trebaju i sinus i kosinus. [ SrdjanR271 @ 02.12.2011. 18:29 ] @
Pošto si u pričio o kompleksnim brojevima, izložiću ti kako ja to računam.
Ne znam napamet sve one formule tipa:

Tebi se uvek traži  .
Primer 1.

Znači ne uradiš ovako 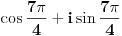
Zapamti ovo.
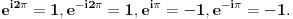
Mada ovo uvek možeš izračunati preko Ojlerove formule 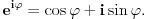
A ako se radi baš o npr. ovome 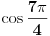 , imaš trigonometrijski krug, adicione formule ili šta god hoćeš.
Ali ako je  , uvek možeš da u eksponentu rastaviš taj ugao.
[Ovu poruku je menjao SrdjanR271 dana 02.12.2011. u 19:51 GMT+1][ Sonec @ 02.12.2011. 18:39 ] @
Citat: SrdjanR271:
Ne zanm napamet sve one formule tipa:
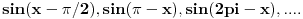
Pa naravno da te formule ne treba da se uce napamet, to se lako izvede za 30 sekundi sa trigonometrijskog kruga il na neki drugi nacin. [ SrdjanR271 @ 02.12.2011. 18:45 ] @
Citat: Sonec: Pa naravno da te formule ne treba da se uce napamet, to se lako izvede za 30 sekundi sa trigonometrijskog kruga il na neki drugi nacin.
Naravno.
Ja sam hteo samo da kažem, da ne mora ni da ih zna ni izvodi, jer je lakše raditi u exp obliku. [ patkan92 @ 02.12.2011. 18:45 ] @
Ja mislim da necu smeti na kolokviju da radim preko Ojlerove formule, ali to ne znaci da na ovaj nacin necu moci da dodjem do ugla samo :) Ovako mi je mnogo jasnije. Hvala Srdjane! I imam jos pitanje sada, posto si dobio 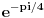 . A ovde  kod kosinusa nema minus jer je funckija parna, a ispred sinusa ide minus zato sto je funkcija neparna. Je l sam u pravu?
Sonec, mozes li mi detaljno objasniti kako se izvode te formule, kako se gledaju uglovi, kako da znam u kom je kvadrantu na primer  , kako da posle to svedem na prvi kvadrant? (posto mi gledaju i postupak, pa cu morati i to morati da pisem sve detaljno...kako sam dosao do tog ugla...) [ Sonec @ 02.12.2011. 18:48 ] @
Citat: patkan92
Sonec, mozes li mi detaljno objasniti kako se izvode te formule, kako se gledaju uglovi, kako da znam u kom je kvadrantu na primer  , kako da posle to svedem na prvi kvadrant? (posto mi gledaju i postupak, pa cu morati i to morati da pisem sve detaljno...kako sam dosao do tog ugla...)
Posto si mi se direktno obratio sa molbom, onda moram da odgovorim. Ne mogu sad da ti to objasnjavam, imam sutra kolokvijum iz Analize 2a pa moram da posvetim tome paznju. Objasnicu ti sutra posle kolokvijuma ako to ne uradi neko pre.
A verujem da ces i na googlu/matematiranje/... naci nesto. [ SrdjanR271 @ 02.12.2011. 18:50 ] @
Mislim da smeš da koristiš Ojlerovu formulu.
Vidi u svesci ili skripti, zbirci, pominju li eksponencijalni oblik kompleksnog broja?
A to što si pitao jeste zbog neparnosti sinusa.
[ patkan92 @ 02.12.2011. 19:00 ] @
Sonec, nije problem. Sacekacu do sutra, nije mi bas hitno. Kolokvijum mi je 10. Dec, tako da imam vremena. :)
Srdjane, nismo radili to ni na vezbama, ni na predavanju. Mislim da bi mi pravili problem oko toga. Samo nesto da te pitam, je l je ispravno ovako za 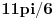 :
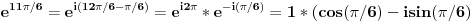 ? [ SrdjanR271 @ 02.12.2011. 19:05 ] @
Citat: patkan92: Samo nesto da te pitam, je l je ispravno ovako za 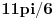 :
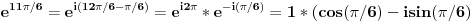 ?
Da. [ patkan92 @ 02.12.2011. 19:18 ] @
A za 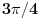 bilo bi: 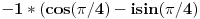 ?
I jos jedno pitanje, ako dobijem u prvom kvadrantu ugao, je l opet stavljam minus ispred 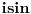 zbog neparnosti ili tada ostaje plus 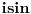 ?
A radili smo nesto i kao: nacrtamo prvo u kom se kvadrantu nalazi  , i onda ako ne dobijemo isti ugao posle racuna, dodaje se uvek 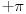 na taj dobijeni ugao da bi se kvadranti poklopili. O cemu je tu rec? Toga se bas ne secam dobro sa predavanja, zasto se zapravo dodaje to 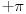 ? [ SrdjanR271 @ 02.12.2011. 19:24 ] @
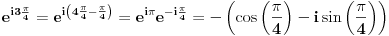
Tako si i ti dobio.
Ako imaš sin(-ugao)=-sin(ugao).
Citat: patkan92: i onda ako ne dobijemo isti ugao posle racuna, dodaje se uvek 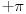 na taj dobijeni ugao da bi se kvadranti poklopili. O cemu je tu rec? Toga se bas ne secam dobro sa predavanja, zasto se zapravo dodaje to 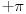 ?
Isti kao koji? [ patkan92 @ 02.12.2011. 19:32 ] @
Vidis u prvom postu ovu sliku gde kordinate x i y daju ugao u cetvrtom kvadrantu, e pa sada ako se negde (ne secam se gde) u zadatku ne poklope kvadranti (znaci neki ugao tokom racunanja) onda se dodaje to 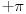 na taj dobijeni ugao tokom racunanja... Ne znam bolje da objasnim, jer se i sam ne secam o cemu se radi. :/ [ cikin @ 02.12.2011. 21:18 ] @
http://www.slideshare.net/mArKoBK3/trigonometrijske-formule imas tu objasnjeno, pogledaj malo...pa jednostavno vidis da su to kao ose x,y oko kojeg se opisuje jedinicni krug, same ose dele krug na 4 dela-kvandrante, a imas u tu kako se svodi na prvi, mada ti je bolje da ne ucis to napamet, vec da shavtis kako se to dobija, jer nije tesko....
[ patkan1992 @ 03.12.2011. 17:27 ] @
Srdjane, sada sam se setio. Asistentkinja je rekla ovako: "Kada nacrtamo skicu, vidimo u kom se kvadrantu nalazi tacka x i y koordinata, zatim izracunamo ugao 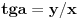 . I ako se taj ugao koji izracunamo ne poklapa sa slikom (znaci ako nisu u istom kvadrantu), mi treba da dodamo 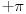 na 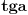 .
Zasto zapravo treba da se dodaje to 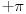 ? [ Sonec @ 03.12.2011. 17:51 ] @
Zato sto je vrednost tangesa u prvom i trecem, odnosno drugom i cetvrtom kvadrantu ista.
A takodje, znas da tanges funkcija ima 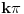 period, pa se vrednost tangesa od tog ugla nece promeniti. [ patkan1992 @ 03.12.2011. 17:54 ] @
A je l je bas neophodno da dodam to 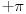 ako se 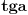 ne poklopi sa uglom na slici? Cemu dodavanje 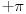 ako se vrednost ne menja? [ Sonec @ 03.12.2011. 17:57 ] @
Ne, bolje dodaj 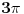 .
Naravno da treba da dodas  da bi dobio tacno resenje.
Dodajes  da bi nasao tvoj ugao  . Ne menja se vrednost tangesa, al ce se promeniti vrednost sinusa i kosinusa kad budes koristio Moavrovu formulu. [ patkan1992 @ 03.12.2011. 18:08 ] @
U zadatku koji sam postavio u prvom postu, 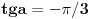 , to je cetvrti kvadrant?
Kako se ovo gleda? Kako da znam da je 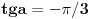 bas u cetvrtom kvadrantu? [ Sonec @ 03.12.2011. 18:17 ] @
Nije 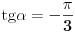 , vec je 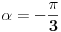 .
Kako znas u kom je kvadrantu, pa lako, nacrtas taj ugao na trigonometrijskom krugu i vidis. Ako te zbunjuju radijani, ti prebaci u stepene i onda vidi. [ patkan1992 @ 03.12.2011. 18:24 ] @
Upss, da.
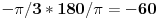 I kako odavde da znam gde se nalazi ugao od -60 stepeni? [ Sonec @ 03.12.2011. 18:27 ] @
-60 je (na trigonometrijskom krugu) ugao od 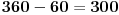 stepeni.
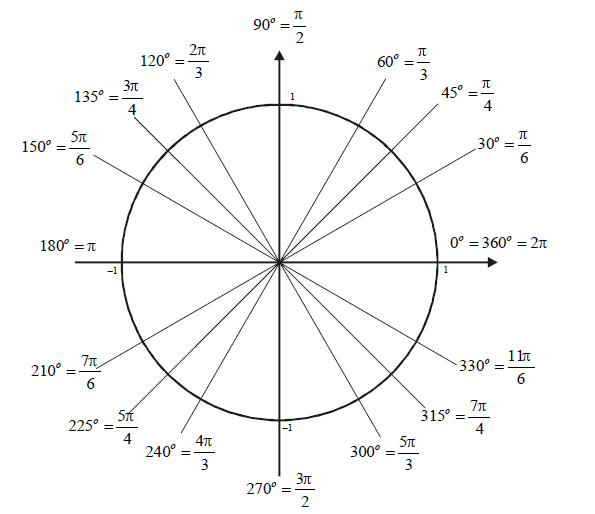 [ patkan1992 @ 03.12.2011. 18:31 ] @
A kada bi se dobio neki ugao u trecem kvadrantu, kako bi za njega znao da je bas u trecem? Koji ugao minus taj dobijeni?
[ Sonec @ 03.12.2011. 18:35 ] @
Jedva sam shvatio sta pitas...
Pa sve zavisi, ugao od 200 stepeni je u trecem kvadrantu, a takodje je npr. i ugao -100 u trecem kvadrantu.
Kad je ugao pozitivan, ti onda direktno gledas gde je, a kad je negativan, ti onda mu dodas 360 stepeni i onda gledas gde je, konkretno u drugom primeru 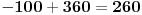 [ patkan1992 @ 03.12.2011. 18:37 ] @
Kad je pozitivan, tada mi nije problem. Lose sam formulisao pitanje... Hteo sam da pitam, da li kada je ugao negativan uvek treba da se doda 360 stepeni? Konkretno sam ciljao na to da se za druge uglove mozda dodaje 180 stepeni (ne znam iz kog razloga, ali bolje da pitam, nego da se zeznem na kolokvijumu).
[ Sonec @ 03.12.2011. 18:39 ] @
Citat: Sonec:
Kad je ugao pozitivan, ti onda direktno gledas gde je, a kad je negativan, ti onda mu dodas 360 stepeni i onda gledas gde je Citat: patkan1992 Konkretno sam ciljao na to da se za drugo uglove mozda dodaje 180 stepeni (ne znam iz kog razloga, ali bolje da pitam, nego da se zeznem na kolokvijumu).
Nemoj dodavati 180 stepeni kad je negativan, radi kako sam ti rekao.
[ patkan1992 @ 03.12.2011. 18:41 ] @
To sam hteo da pitam. Hvala puno po ne znam koji put! :)
[ patkan1992 @ 04.12.2011. 11:56 ] @
Da ne otvaram novu temu, sto se tice ovog ugla (tj. znakova kod sinusa i kosinusa):
Prvo da vas pitam da li ja moram da primenim odmah ono da je kosinus parna, a sinus neparna funkcija? Ili mogu da pisem ovako (npr.):
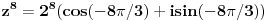 ?
I onda kada treba da izracunam taj ugao bice (pa posle ovoga odmah napisem koliko je 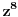 u odnosu na to koje sam uglove dobio):
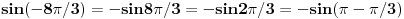 , i sada mi ovde pise (ovo mi je zadatak sa vezbi) da je 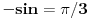 , zasto nije 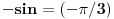 ? To me buni... Jer je kod kosinusa ovako:
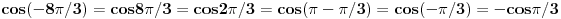 .
Da l je ovo opet oko toga zato sto je sinus neparna funkcija, ako bi neko mogao da mi objasni zasto je bas tako... [ Sonec @ 04.12.2011. 15:09 ] @
Citat: patkan1992: Da ne otvaram novu temu, sto se tice ovog ugla (tj. znakova kod sinusa i kosinusa):
Prvo da vas pitam da li ja moram da primenim odmah ono da je kosinus parna, a sinus neparna funkcija?
Ne moras, koristis kad ti ta osobina sinusa/kosinusa pomaze pri racunu.
Citat: patkan1992: Ili mogu da pisem ovako (npr.):
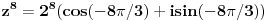 ?
Mozes da napises u bilo kom obliku, samo da je tacno. E sad, ako moze da se sredi jos, onda bi valjalo srediti.
Citat: patkan1992:
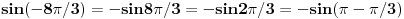 , i sada mi ovde pise (ovo mi je zadatak sa vezbi) da je 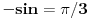 , zasto nije 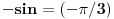 ?
Kako uopste mozes da pises nesto ovako: 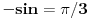 , zasto nije 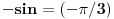 . Vazi sledece: 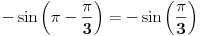
Citat: patkan1992:To me buni... Jer je kod kosinusa ovako:
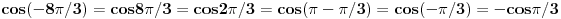 .
Ovako 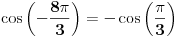 i 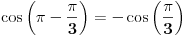 , ali 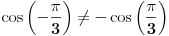 i 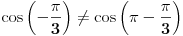
I da, na nekim mestima se koristila parnost i neparnost trigonometrijskih funkcija. [ patkan1992 @ 04.12.2011. 15:32 ] @
Bunio me je ovaj minus ispred sinusa, i posle onaj minus u 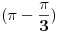 , razmisljao sam da taj minus iz zagrade izlazi ispred sinusa i menja mu znak (menja znak vec postojecem minusu ispred sinusa koji je posledica neparnosti sinusa). Znaci ovako nesto:
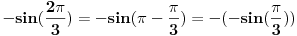 ---> Znaci kao sto je minus izasao kod kosinusa ispred. Ovo je verovatno jako glupo, ali tako sam razmisljao pa sam zato i napisao prethodni post da bi mi neko razjasnio zasto pogresno razmisljam....
P.S. Da ne otvaram novu temu, mozes li da mi das neki fajl o Nizovima? Ono na matematiranju i nije bas detaljno objasnjeno, nista ne razumem... [ matematikuvolim @ 04.12.2011. 15:38 ] @
Sta ce ti nizovi u 2. razredu srednje?
[ Sonec @ 04.12.2011. 15:39 ] @
Ako ima nesto da te buni jos kod trigonometrije ti pitaj :)
Teorija ili zadaci iz nizova?
[ patkan1992 @ 04.12.2011. 16:00 ] @
Citat: Sta ce ti nizovi u 2. razredu srednje?
Na fakultetu sam... :)
Citat: Teorija ili zadaci iz nizova?
Teorija pre svega, da bih shvatio o cemu se tu radi. A zadatke bih posle radio. [ Sonec @ 04.12.2011. 16:09 ] @
Poslao sam ti link na PM. To je zbirka, al imas i sasvim dovoljno teorije.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|
 kod kosinusa i sinusa. Mozda su izvukli minus, ali ne razumem kako. :/
kod kosinusa i sinusa. Mozda su izvukli minus, ali ne razumem kako. :/
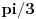


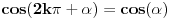

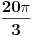

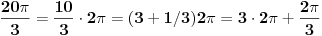
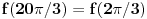

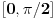
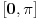

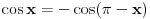
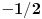


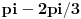

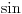
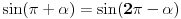
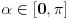


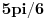



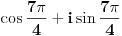
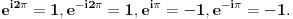
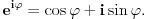
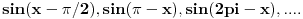
 kod kosinusa nema minus jer je funckija parna, a ispred sinusa ide minus zato sto je funkcija neparna. Je l sam u pravu?
kod kosinusa nema minus jer je funckija parna, a ispred sinusa ide minus zato sto je funkcija neparna. Je l sam u pravu?