[ matematikuvolim @ 02.12.2011. 16:49 ] @
| U kompleksnoj analizi ako je prvi izvod neprekidan, neprekidan je i peti. Sto nije tako u Analizi 1? |
|
[ matematikuvolim @ 02.12.2011. 16:49 ] @
[ Nedeljko @ 02.12.2011. 18:44 ] @
To je posledica Koši-Rimanovih uslova. Naime, realan ili imaginaran deo diferencijabilne kompleksne funkcije posmatran kao realna funkcija dve realne promenljive nije samo diferencijabilna funkcija dveju realnih promenljivih, nego i harmonijska funkcija - tj. funkcija čiji je laplasijan (zbir drugih izvoda po x i drugih izvoda po y) jednak nuli. Iz tog uslova sledi neograničena diferencijabilnost. U slučaju realnih funkcija jedne realne promenljive ovaj uslov se dvodi na to da je drugi izvod jednak nuli, odnosno da se radi o linearnoj funkciji.
[ SrdjanR271 @ 02.12.2011. 18:53 ] @
[ matematikuvolim @ 02.12.2011. 18:57 ] @
A u analizi 1 ja ne mogu analiticku funkciju da kazem da je mogu uvek razviti u st red?
[ SrdjanR271 @ 02.12.2011. 19:16 ] @
[ matematikuvolim @ 02.12.2011. 19:29 ] @
Pa zar to nije potpuno analogna prica sa kompleksnom analizom? Ako fja ima neprekidan prvi izvod negde u nekom delu kompleksne ravni onda su joj u tom delu neprekidni i 22 i 57 i 88 izvod, svi izvodi.
[ SrdjanR271 @ 02.12.2011. 19:39 ] @
Citat: matematikuvolim: Pa zar to nije potpuno analogna prica sa kompleksnom analizom? Ako fja ima neprekidan prvi izvod negde u nekom delu kompleksne ravni onda su joj u tom delu neprekidni i 22 i 57 i 88 izvod, svi izvodi. Donekle. Tu je prvi neprekidan a onda i ostali. U realnoj to ne mora da važi. Npr. 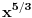 ima neprekidan prvi izvod u nuli, dok drugi nije. ima neprekidan prvi izvod u nuli, dok drugi nije.[ matematikuvolim @ 02.12.2011. 19:40 ] @
Moje pitanje je da li se analiticnost drugacije definise od analize do analize?
[ SrdjanR271 @ 02.12.2011. 19:49 ] @
Ja bih rekao da.
Ja znam da se u kompleksnoj do Tejlorovog reda dolazi preko Košijeve integralne formule. Tako nešto u realnoj ne bi moglo, jer je Košijeva integralna formula stvar čisto kompleksne analize. Žurim sad, pa ću na eventualna pitanja odgovoriti oko 3 noćas. [ matematikuvolim @ 02.12.2011. 20:32 ] @
Kako se definise analiticka funkcija u analizi 1, a kako u analizi 2?
[ Sonec @ 02.12.2011. 20:54 ] @
Analiza 1:
Za funkciju  koja je jednaka zbiru svog Tejlorovog reda u okolini tacke koja je jednaka zbiru svog Tejlorovog reda u okolini tacke  , ili, kako se jos kaze, koja se moze razviti u stepeni red u okolini tacke , ili, kako se jos kaze, koja se moze razviti u stepeni red u okolini tacke  kaze se da je analiticka u okolini tacke kaze se da je analiticka u okolini tacke  . Jasno je da ce funkcija . Jasno je da ce funkcija  biti analiticka ako, osim toga sto je beskonacno diferencijabilna, vazi biti analiticka ako, osim toga sto je beskonacno diferencijabilna, vazi 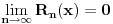 , gde je , gde je 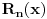 ostatak u Tejlorovoj formuli ostatak u Tejlorovoj formuli 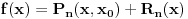 . .Matematicka Analiza 1 D.Adnadjevic, Z.Kadelburg U knjizi za Matematicku Analizu 2 (isti autori) nisam nasao (ne tvrdim da nema). [ Nedeljko @ 02.12.2011. 21:24 ] @
U realnoj analizi se stepeni red sa više promenljivih definiše analogno slučaju jedne promenljive i preko njega pojam analitičke funkcije.
U kompleksnoj analizi iz postojanja prvog izvoda sledi da postoje svi izvodi i da je štaviše funkcija analitička. U realnoj analizi iz postojanja prvog izvoda ne sledi ni postojanje drugog izvoda. Razlika je u Koši-Rimanovim uslovima. U kompleksnoj analizi postoji veza između realnog i imaginarnog dela diferencijabilne funkcije iz koje sledi da realni i imaginarni deo posmatrani kao realne funkcije nisu samo diferencijabilne, već i harmonijske funkcije. Za harmonijske funkcije se dokazuje da su uvek analitičke na sličan način kao u kompleksnoj analizu - prvo se dokaže Košijeva integralna formula za slučaj konveksnih oblasti, pa onda iz Košijeve integralne formule da su i analitičke. E, odatle već sledi beskonačna diferencijabilnost. [ Nedeljko @ 02.12.2011. 21:37 ] @
Samo da napomenem da se realni analogon Košijeve integralne formule za realne harmonijske funkcije zove svojstvo srednje vrednosti.
[ matematikuvolim @ 03.12.2011. 04:30 ] @
Citat: Sonec: Analiza 1: Za funkciju  koja je jednaka zbiru svog Tejlorovog reda u okolini tacke koja je jednaka zbiru svog Tejlorovog reda u okolini tacke  , ili, kako se jos kaze, koja se moze razviti u stepeni red u okolini tacke , ili, kako se jos kaze, koja se moze razviti u stepeni red u okolini tacke  kaze se da je analiticka u okolini tacke kaze se da je analiticka u okolini tacke  . Jasno je da ce funkcija . Jasno je da ce funkcija  biti analiticka ako, osim toga sto je beskonacno diferencijabilna, vazi biti analiticka ako, osim toga sto je beskonacno diferencijabilna, vazi 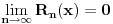 , gde je , gde je 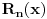 ostatak u Tejlorovoj formuli ostatak u Tejlorovoj formuli 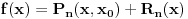 . .Matematicka Analiza 1 D.Adnadjevic, Z.Kadelburg U knjizi za Matematicku Analizu 2 (isti autori) nisam nasao (ne tvrdim da nema). Po meni odavde posto je izvod stepenog reda stepeni red i u Analizi 1 sledi da ako je funkcija analiticka ima neprekidne sve izvode. [ Nedeljko @ 03.12.2011. 09:27 ] @
Sad je meni jasno šta tebe buni.
I u realnoj i u kompleksnoj analizi ako je neka funkcija diferencijabilna (u nekoj tački), onda je neprekidna (u toj tački). U realnoj analizi iz postojanja prvog izvoda ne sledi ni neprekidnost prvog izvoda, a kamoli postojanje izvoda višeg reda. Stoga diferencijabilna funkcija ne mora biti analitička. U kompleksnoj analizi iz postojanja izvoda sledi da je funkcija analitička. U oba slučaja, ako je funkcija analitička, odatle sledi da postoje svi izvodi, a pošto je izvod reda n+1 izvod izvoda reda n, odatle sledi da je izvod reda n diferencijabilan, onda je i neprekidan. [ matematikuvolim @ 04.12.2011. 12:02 ] @
Sam mi je jasnije. Hvala Nedeljko. A kako da znam da ako ima izvod u nekoj tacki oblasti D, da onda ima izvod u svim tackama D? Mislim na kompleksnu analizu. Ima li neki lak zakljucak toga. Hvala jos jednom.
[ Nedeljko @ 04.12.2011. 17:50 ] @
Diferencijabilnost na skupu tačaka se definiše kao diferencijabilonost u svakoj tački tog skupa. U principu, zadaci se rade posle teorijskih osnova i tu ti je glavna greška.
[ matematikuvolim @ 06.12.2011. 20:10 ] @
Citat: Nedeljko: Diferencijabilnost na skupu tačaka se definiše kao diferencijabilonost u svakoj tački tog skupa. U principu, zadaci se rade posle teorijskih osnova i tu ti je glavna greška. Citat: Nedeljko: Sad je meni jasno šta tebe buni. I u realnoj i u kompleksnoj analizi ako je neka funkcija diferencijabilna (u nekoj tački), onda je neprekidna (u toj tački). U realnoj analizi iz postojanja prvog izvoda ne sledi ni neprekidnost prvog izvoda, a kamoli postojanje izvoda višeg reda. Stoga diferencijabilna funkcija ne mora biti analitička. U kompleksnoj analizi iz postojanja izvoda sledi da je funkcija analitička. U oba slučaja, ako je funkcija analitička, odatle sledi da postoje svi izvodi, a pošto je izvod reda n+1 izvod izvoda reda n, odatle sledi da je izvod reda n diferencijabilan, onda je i neprekidan. Samo sam trazio objasnjenje za boldovan deo. Citam teoriju i imam problema. Negde pise funkcija je analiticka ako ima neprekidan prvi izvod. Negde kaze pod pojmom analiticka podrazumeva se analiticka svuda sem u konacno mnogo tacaka. Kako onda iz postojanja izvoda sledi da je i neprekidan. Kako moze biti neprekidan ako postoje singulariteti u konacno mnogo tacaka? [ Nedeljko @ 07.12.2011. 09:56 ] @
Citat: matematikuvolim: Negde pise funkcija je analiticka ako ima neprekidan prvi izvod. To nije definicija, već teorema kompleksne analize. Takođe, Gursa je uspeo da dokaže da je izvod kompleksne diferencijabilne funkcije u oblasti uvek neprekidan. To je takođe teorema. Citat: matematikuvolim: Negde kaze pod pojmom analiticka podrazumeva se analiticka svuda sem u konacno mnogo tacaka. Citiraj šta tačno piše u knjizi. Uzgred, ako je u pitanju knjiga Vojina Dajovića, možeš slobodno da je baciš. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|