Pomocu Bezuovog stava. Nadjes nule polinoma i rastavis.

Sta sa cim treba ovde da delim?

Ako je nula polinoma (tj. ) onda deli .
Priseti se Bezuovog stava, valjace ti.

Znaci gledam slobodan clan, i brojeve sa kojima je on deljiv? A mi je broj koji je menjanjem u polinomu dao P(x)=0?

Mrzelo me da pisem....

I ti brojevi 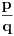su ti potencijalne nule polinoma, svaku od njih uvrstis u polinom umesto , i ako je polinom tada jednak nuli, onda si nasao jednu nulu tog polinoma. Ovde u tesktu koji sam okacio pise sta potencijalna nula polinoma mora da zadovoljava.
Al ja ne bih uopste tako trazio nule, pokusas nagadjanjem da nadjes nulu polinoma, probas sa i vidis dal ce da upali...


_{[Ovu poruku je menjao Sonec dana 03.12.2011. u 19:19 GMT+1]}

Shvatio :) Hvala puno!

Samo da dodam, isti efekat si mogao da postignes malim sredjivanjem determinante:
npr. da pomnozis drugi red sa -1 i dodas na prvi: lako se vidi da mozes (a-1) da izvuces kao zajednicki;
Itd. Na taj nacin mozes dobiti kompletno rastavljanje na cinioce.

Zavisi od situacije, ako tako "sredjivanje" determinante nije bas ocigledno, moze i tako kako je ranije pisano.
S' druge strane, na ovaj nacin dobijas ne samo lakse rastavljanje nego i dobijanje vrednosti same determinante.

Najelegantnije je da determinantu ne izračunava Sarusovim pravilom već razvijanjem preko kofaktora.
Tako bi u sva tri člana imao (a-1) kao zajednički faktor.